数交点, 估长度?

任意给出平面上的一条可求长曲线, 比如, 我们在纸上随手画的一条的曲线, 在不知道这条曲线具体的方程的情况下, 有没有什么简单的好办法能够比较精确的估计这条曲线的长度呢? 这里给出一个方法, 让我们数交点数量, 就能估计曲线长度.

可求长曲线长度的近似估计

具体操作

我们按照以下步骤来做:

• 以某一固定的间距 $r$ 画出一族平行线;
• 将这一族平行线旋转 $\frac{\pi}{4}$, $\frac{\pi}{2}$, $\frac{3\pi}{4}$, 这样我们一共得到四族平行线;
• 数出这四族平行线与待求长曲线的交点数量 $n$;
• 按如下公式计算曲线近似长度 $$L = \frac{1}{2}nr\frac{\pi}{4}.$$

也许见到这个公式, 大家会有一点觉得不可思议, 我们可以拿一个简单的例子来试一试, 增强一下信心.

举个栗子

1. 我们就用圆来做为第一个例子吧. 半径为 $r$ 的圆, 其周长显然为 $2\pi r$. 按以上方法做四族平行线, 间距就取为 $r$.
   

   用圆来举个栗子

   
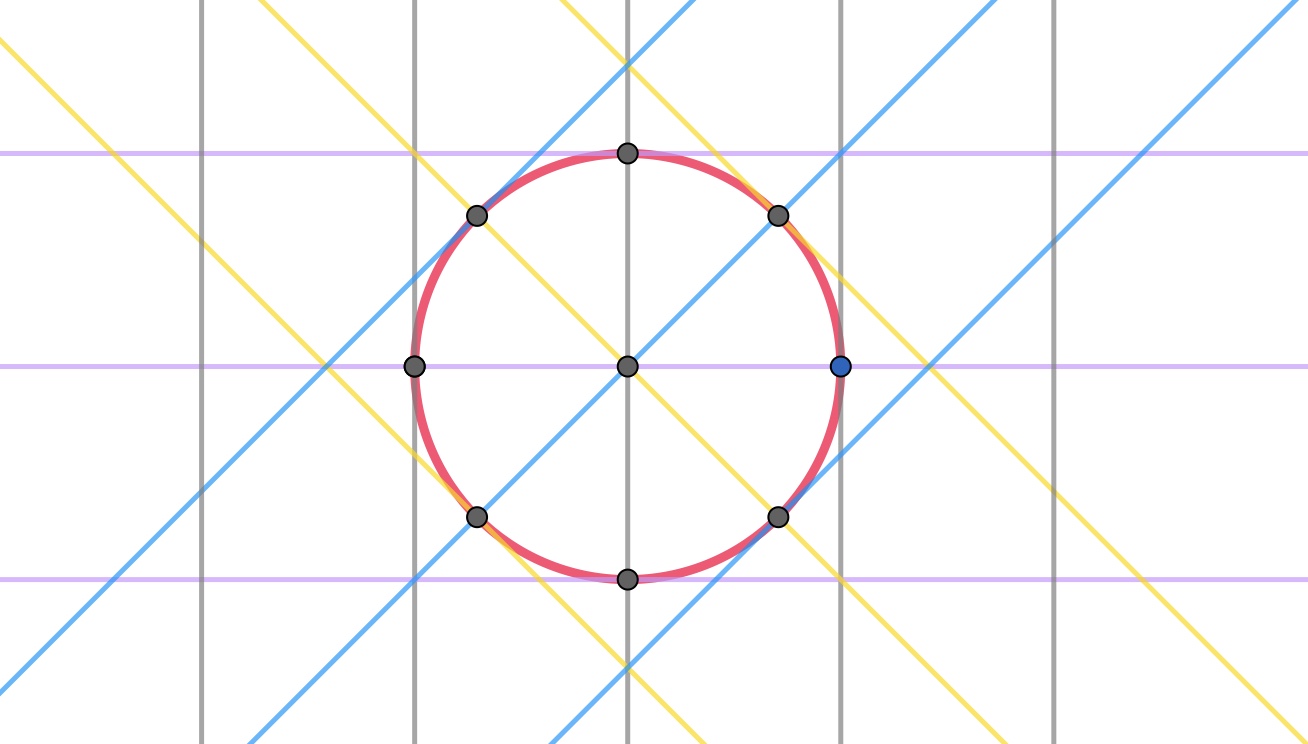
   显然, 圆和这 4 族平行线总共有 16 个交点, 于是用上述公式计算
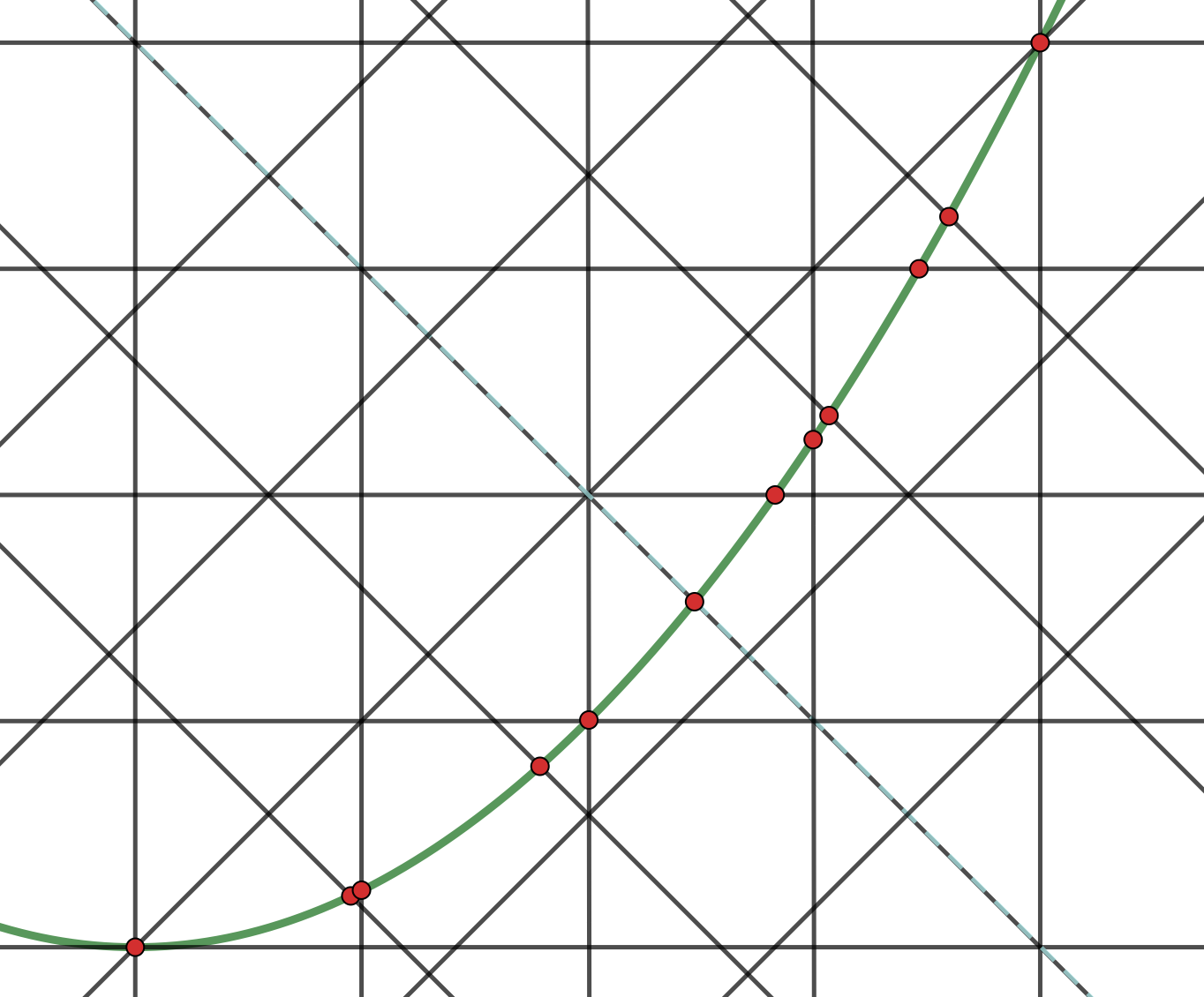
   $$L = \frac{1}{2}16r\frac{\pi}{4} = 2\pi r .$$

2. 再来一个复杂一点的例子. 取 $y = x^2$ 在 $[0, 1]$ 上这一段的曲线. 由曲线长度的计算公式 $L = \int_{x_1}^{x_2}\sqrt{x’^2 + y’^2}dx$ 可以计算出 $L \approx 1.4789…$. 用以上给出来的方法, 比如取间距为 $1/2$, 做出 4 族平行线, (如下图)数出 11 个交点, 于是得到 $$L = \frac{1}{2}11\cdot \frac{1}{2}\frac{\pi}{4} \approx 2.1598…$$ 取间距为 $1/4$, 则数出 17 个交点, 于是得到 $$L = \frac{1}{2}17\cdot \frac{1}{4}\frac{\pi}{4} \approx 1.6689…$$ 其绝对误差在 0.2 左右. 事实上当平行线的间距缩小一些, 更密集, 这个近似估计就越精确.
   

   $y = x^2$

Cauchy-Crofton 公式

以上近似方法看起来很简单, 但其背后是来自于微分几何的相关结果. 这就是 Cauchy-Crofton 公式.

Cauchy-Crofton 公式

设平面上长度为 $L$ 的曲线 $C$. 对于平面上任意一条直线 $l$, 用 $n(l)$ 表示直线 $l$ 与 曲线 $C$ 的交点个数. 我们知道, 给定平面直角坐标系 $Oxy$, 任意直线的法式方程都可以表示为
$$x \cos\theta + y\sin\theta = p\qquad p\geqslant0, 0\leqslant\theta\leqslant 2\pi.$$
于是可以认为, 每一条直线都是平面空间 $E:=(\theta, p)$中的点, 交点数 $n(l)$ 是一个二元函数 $n(\theta, p)$.

【Cauchy-Crofton 公式】 $$\begin{equation}\label{eq:CC}L = \frac{1}{2}\iint_{E}n(\theta, p)d\theta dp.\end{equation}$$

事实上, 由于平面上所有与曲线相交的直线只是 $E$ 的一部分, 构成一个区域, 记为 $D$. 显然, 在 $D$ 以外的部分上述积分值为 $0$. 所以我们只需要考虑
$$L = \frac{1}{2}\iint_{D}n(\theta, p)d\theta dp.$$

近似计算方法的解释

利用 Cauchy-Crofton 公式, 以上近似计算曲线弧长的步骤, 便有了
$$\frac{1}{2}\iint_{D}n(\theta, p)d\theta dp \approx \frac{1}{2}\sum_{i}n(\theta, p)\Delta\theta_i \Delta p_i$$
按以上方法取的四族平行线, 显然 $\Delta\theta_i =\frac{\pi}{4}$, $\Delta p_i = r$ , 于是便有了近似公式 $L = \frac{1}{2}nr\frac{\pi}{4}.$. 换一种平行线族的取法, 可以得到相应的计算公式.

公式的证明

为了完整性, 在这里将叙述 Cauchy-Crofton 公式的证明. 证明分为四步, 从最简单的情况开始讨论.

1. 设曲线是 $x$-轴上的线段, 位于 $[-L/2,L/2]$ 上, 显然与其相交的直线对应的点构成的区域 $D$ 为 $[0,\frac{L}{2}|\cos\theta|]\times [0, 2\pi)$, 而每条直线与其只有一个交点, 即 $n(\theta, p)=1$. 故
   $$\begin{array}{cl} \frac{1}{2}\iint_{D}n(\theta, p)d\theta dp &=& \frac{1}{2}\iint_{D}d\theta dp\\ &=& \frac{1}{2}\cdot 4 \int_{0}^{\frac{\pi}{2}}\frac{L}{2}|\cos\theta|d\theta\\ &=& L \end{array}$$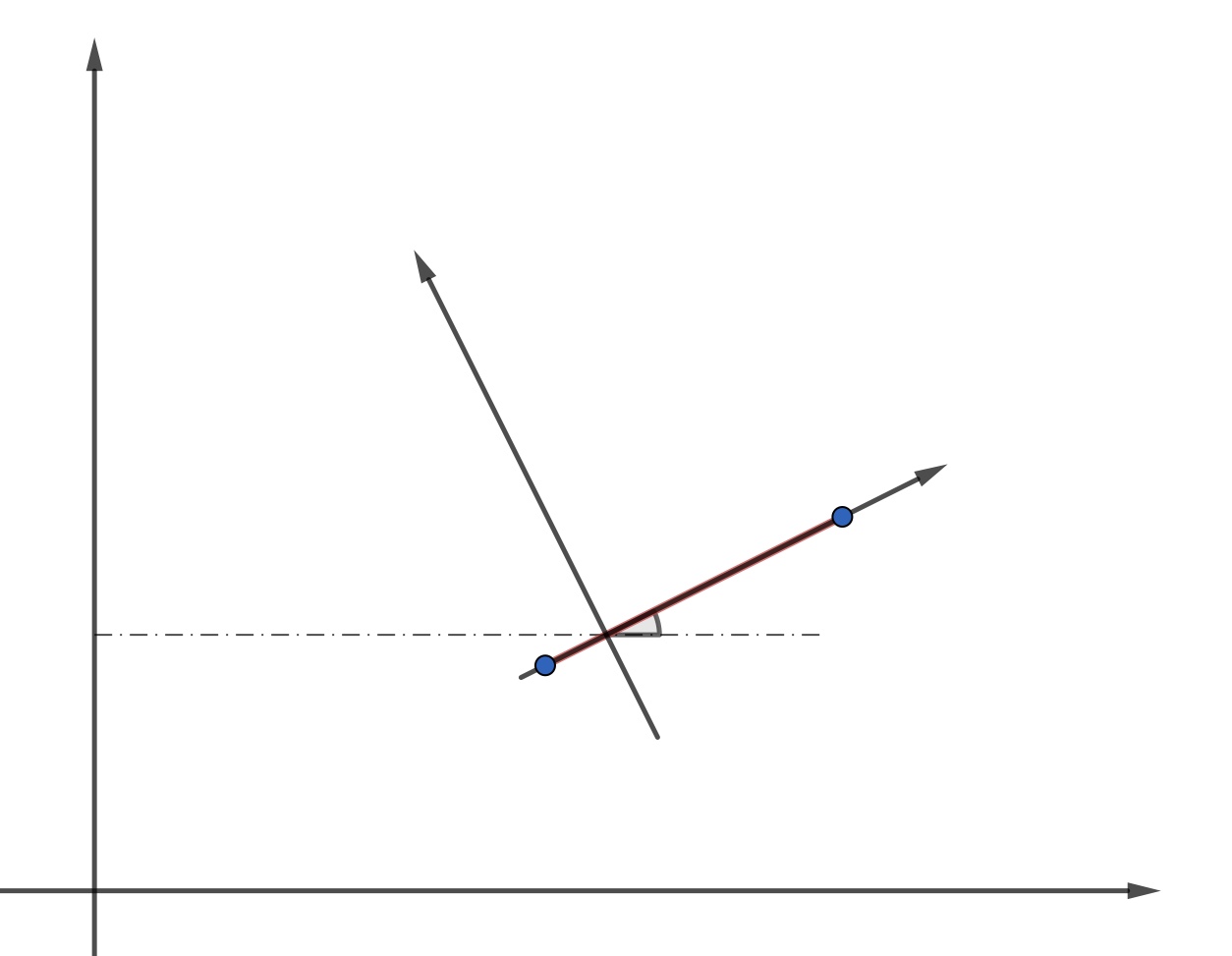

2. 依旧设曲线 $C$ 为直线段, 但并不位于坐标轴上. 则以 $C$ 为坐标轴可以构建新的直角坐标系 $O’x’y’$. 并且两坐标系之间满足线性变换 $$\begin{cases} x’ = x\cos\alpha +y\sin\alpha + a\\ y’ = -x\sin\alpha +y\cos\alpha + b \end{cases}$$ 由此得到在新坐标系下的直线方程, 以及两个方程之间的变换关系. 容易计算, 其 Jacobi 行列式的值为 $1$. 按照积分的变量代换公式, 类似 1 中的计算, 求出 ($\ref{eq:CC}$) 式的值为 $L$.

3. 设曲线 $C$ 为有限条直线段所组成的折线. 不失一般性, 考察由两条直线段构成的折线, 然后归纳推得结结论.
   折线段的两部分分别表示为 $C_1$, $C_2$, 其长度分别为 $L_1$, $L_2$ 满足 $L_1+L_2=L$. 曲线 $C$ 相应的区域 $D$ 显然满足 $D = D_1\cup D_2$, 其中 $D_1, D_2$ 是两条直线段分别相应的区域.
   于是, 由上面第 2 步, 我们有
   $$\begin{array}{c}\frac{1}{2}\iint_{D_1}d\theta dp = L_1\\ \frac{1}{2}\iint_{D_2}d\theta dp = L_2\end{array}$$
   而 $D_1$, $D_2$ 必然存在相交的部分 $D_1\cap D_2$, 在这部分上, $n(\theta,p)=2$. 所以 $$\begin{array}{cl} & &\frac{1}{2}\iint_{D_1}d\theta dp +\frac{1}{2}\iint_{D_2}d\theta dp\\ &=& \frac{1}{2}\iint_{D_1/D_2}d\theta dp + 2\cdot\frac{1}{2}\iint_{D_1\cap D_2}d\theta dp + \frac{1}{2}\iint_{D_2/D_1}d\theta dp\\ &=&\frac{1}{2}\iint_{D_1/D_2}d\theta dp + \frac{1}{2}\iint_{D_1\cap D_2}2d\theta dp + \frac{1}{2}\iint_{D_2/D_1}d\theta dp\\ &=& \frac{1}{2}\iint_{D}nd\theta dp = L_1+L_2 = L. \end{array}$$ 于是对于有限条直线段所组成的折线 $C$, 归纳可得
   $$\frac{1}{2}\iint_{D}nd\theta dp = \sum_{i} L_i = L.$$

4. 对于任意可求长曲线, 均可以由折线逼近, 故只需将 3 中的等式推向极限的情况, 这就证明了 Cauchy-Crofton 公式.

推广: 球面上的 Crofton 公式

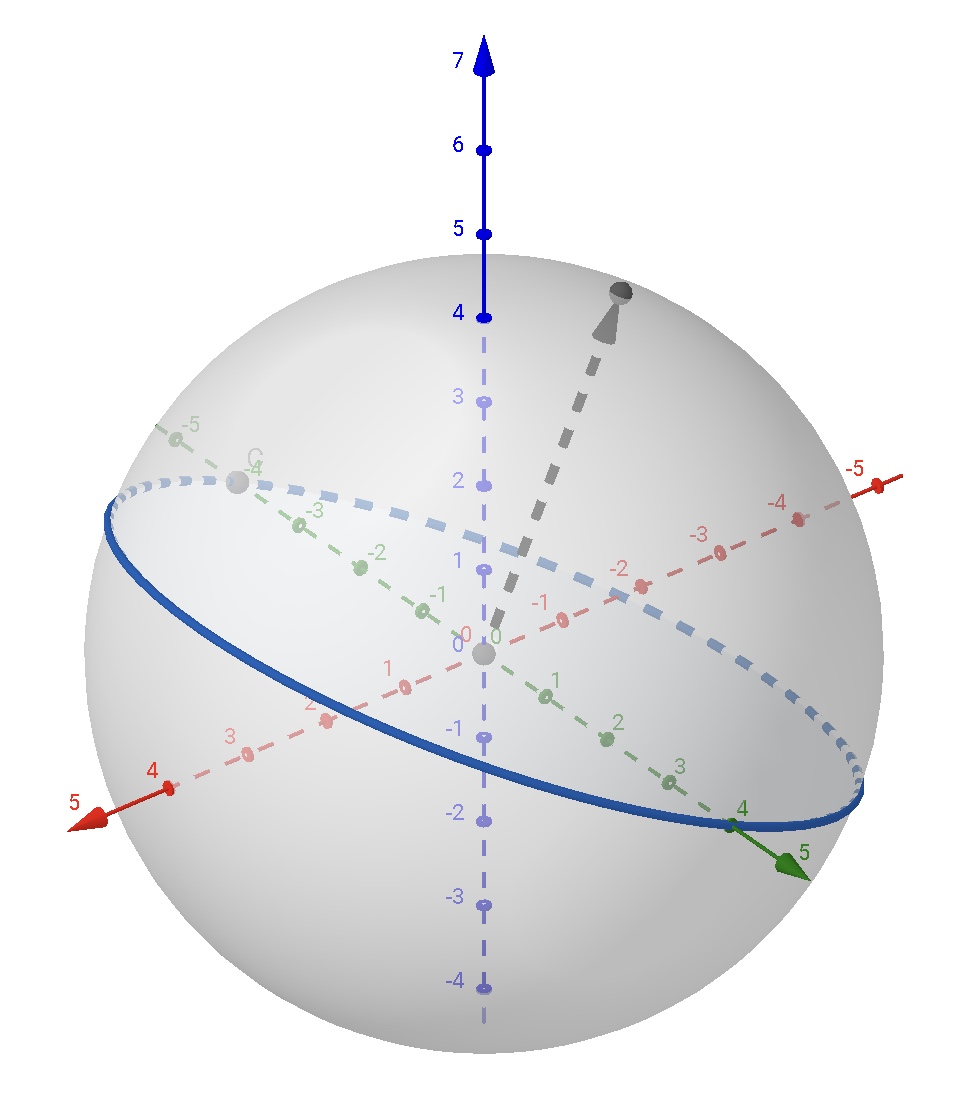
事实上, 平面上的 Cauchy-Crofton 公式可以类似的推广到球面上.

注意到, 球面上的”直线”, 是球上的大圆; 两点确定的”线段”, 是大圆的弧.

我们约定, 指定大圆的方向, 用 $\overrightarrow{w}$ 表示这个大圆所在平面的法向量, 其与大圆的方向构成右旋系. $w$ 表示法向量的末端点(位于球面上), 称为大圆的极点, 显然球面上每个点都唯一的确定了一个定向的大圆.

设 $C$ 为单位球面 $S^2$ 上的曲线, 其长度为 $L$, 大圆与曲线的交点个数记为 $n(w)$, 有以下公式成立:

【球面上的 Crofton 公式】 $$\begin{equation}\label{eq:CCq}L = \frac{1}{4}\iint_{S^2}n(w)dw.\end{equation}$$ 这里 $dw$为球面上的面积微元.

同样的, 上述积分, 在曲线与某些大圆不相交的时候为零, 所以积分区域可以约束到某个区域 $D$ 上, 在其中的每一个点对应的大圆都与曲线相交. 即可以等价的写成
$$L = \frac{1}{4}\iint_{D}n(w)dw.$$

这一公式的证明思想与平面上公式类似, 即: 球面上的曲线, 可以通过”大圆折线”来逼近. 在此不再证明.

尾声

一般本科微分几何学主要内容是经典的内蕴微分几何学, 即探讨几何对象在局部的性质. 而几何对象的整体性质也非常丰富, 并且与局部性质具有紧密的联系, 这部分内容构成整体微分几何. 而这里所谈到的内容, 是平面曲线的整体性质之一, 仅仅是微分几何学中一朵漂亮的小火花.

学无止境, 探索无止境, 数学的世界里还有无数美丽的东西. 我们一起加油向前吧!