关于等周不等式的历史

直接引用文献中对于等周问题的介绍：

最早的几何不等式应该是著名的等周不等式, 该不等式具有悠久的历史. 等周问题最早由著名数学家 Joham Beynoulli 在 1679 年提出, 从等周定理的提出到现在, 人们关于等周问题的研究讨论从未停止过, 研究成果不断的推陈出新, 使得等周型不等式的研究领域欣欣向荣, 可以说等周定理是数学史上被证明次数最多的定理之一…

从实用性的角度来看, 在数学家正式提出等周定理之前, 人类乃至动物界已经在不自觉地使用这个定理了, 比如：人们使用定长的绳子圈地的过程中, 当绳子以圆形的方式圈地时, 得到的土地面积最大; 在寒冷的冬季, 人类或者动物会缩成一团, 为的就是在体积一定的情况下, 尽量缩小自己的表面积, 减小热量的损失；在物理中, 等周不等式问题和跟所谓的最小作用量有关, 一个直观的表现就是水珠的形状, 在没有外力的情况下(如失重的太空舱里), 水珠的形状是完全对称的球体, 这是因为当水珠体积一定时, 表面张力会迫使水珠的表面积达到最小值, 根据等周不等式的原理, 最小值在水珠形状为球状时达到…

等周不等式的一个经典的证明是利用变分方法, 本文中介绍由复分析, 调和分析领域著名数学家 Carleman 给出的复分析证明. 由此出发, 也引出了一系列函数空间理论上的问题之研究.

从属性

首先介绍函数从属性的概念. 这一概念,最早来自于 Lindelöf 在 1908 年给出的一个定理, 现在常称为 Lindelöf 原理.

我们设 $f, g$ 均为 $\mathbb{D}$ 中的解析函数. 若存在解析函数 $\varphi: \mathbb{D}\rightarrow \mathbb{D}$, 使得 $\varphi(0) = 0$ 且 $f = g\circ \varphi$ 对于一切 $z\in \mathbb{D}$ 均成立, 则称 $f$ 从属于 $g$, 记为 $f\prec g$.

事实上, 设 $g(z)$ 为 $\mathbb{D}$ 上的单叶解析函数, 满足$g(0) = 0$. 再设 $f(z)$ 为 $\mathbb{D}$ 上的解析函数, 其满足$f(0) = 0$, 并且 $f$ 的值域落在 $F$ 的值域中. 于是函数 $\varphi(z) = g^{-1} \circ f$ 是 $\mathbb{D}$ 上良定的解析函数, 并且满足 $\varphi(0) = 0$, 以及 $|\varphi(z)|\leqslant 1$. 由 Schwarz 引理, 上述条件等价于要求: $|\varphi(z)|\leqslant |z|$ 且 $f = g\circ w$ 对于一切 $z\in \mathbb{D}$ 均成立.

几何直观上看, $f\prec g$ 意味着对任意的闭圆盘 $\overline{D(0,r)}, r\in(0,1)$ 在 $f = g\circ \varphi$ 作用下的像, 都落在 $g$ 对同一个圆盘作用的像中. 也可以说, 在某种意义下, $f$ 比 $g$ 要”小”. 而 Littlewood 从属定理正是对这一事实的精确表述.

这里记录一些重要的群的例子, 以备参考.

常见的群的例子

这里给出一些重要的群的例子.

关于生成函数, 以下直接引用 wiki 百科上的介绍:

In mathematics, a generating function is a way of encoding an infinite sequence of numbers ($a_n$) by treating them as the coefficients of a formal power series. This series is called the generating function of the sequence.

Unlike an ordinary series, the formal power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the “variable” remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers.

正如这段介绍中所说, 生成函数就是描述数列的另一种不同的方法而已, 这种方法将整个序列视作了一个对象进行考虑, 更具体的说, 就是个幂级数, 其系数有着某些特定含义.

作为一篇小品, 本文只简单介绍一下生成函数定义, 并利用该方法研究斐波那契数列.

在复分析中的几何理论中, 有一个有趣而且重要的主题, 即共形映射. 其中有一类很自然的解析函数类——分式线性变换.

考虑以下有理函数

$$f(z) = \frac{az+b}{cz+d}$$

其中，$a,b,c,d$ 均为复数. 要使得以上函数具有良好的定义, 很自然, 需要要求 $c,d$ 不能同时为 $0$; 另一方面, 为了保证函数不会退化成常数函数, 则需要满足 $a/c \neq b/d$.

综合来说, 当以上有理函数满足 $ad-bc\neq 0$ 时, 我们称之为一个分式线性变换. 我们都知道:

• 分式线性变换的复合还是一个分式线性变换变换.
• 任何分式线性变换都可以表示为三种简单变换的复合, 即:平移、旋转、反演的复合.

关于分式线性变换的很多性质, 留到谈共形映射时再谈. 以下提供一个有意思的视角, 也许能帮助我们更容易的认识分式线性变换.

矩阵的秩

矩阵的秩,是用于描述矩阵的一个重要的性质,它由行(列)向量组的极大线性无关组中包含的向量的个数来定义, 描述了矩阵的行(列)向量空间的维数. 关于一个矩阵 $A$ 的秩,有一点重要基本的性质:

**【定理】** 初等变换不改变矩阵的秩.进一步的,初等行(列)变换不改变矩阵任意列(行)之间的线性相关性.

继续线性代数矩阵部分的笔记。

矩阵的初等变换与分块运算

**定义**【初等变换】 以下三种对矩阵的操作, 每一种都称为对矩阵的进行的一次 **初等变换**. - 将矩阵的一行(列)与另一行(列)交换位置; - 将矩阵的某一行乘以一个非零倍数; - 将矩阵的一行(列)加到另一行(列)上去.

由单位矩阵经过一次初等变换得到的矩阵称为初等矩阵. 关于初等矩阵有以下性质:

从1858年 Cayley 建立起矩阵及其运算以来, 矩阵理论迅速的建立了起来. 矩阵论是数学中内容最丰富, 应用最广泛的部分之一. 矩阵是线性代数中最重要的工具, 贯穿于线性代数的始终. 矩阵论在航空航天, 军事, 信息处理, 人工智能, 金融, 生命科学, 社会科学等很多的领域都有非常重要的作用.

这一部分的笔记将对矩阵理论中的核心内容以及方法进行总结和复习. 假设本笔记的读者, 对于笔记中出现的各种概念并不陌生, 而矩阵定义以及一些运算(加法、乘法、转置)作为基本知识将不在此重述, 笔记将按照一个个独立的知识点组织. 对于一个点的相关知识和方法, 将来自于整个线性代数课程, 以使读者能够综合应用, 融会贯通.

这一部分主要集中讨论定义在闭区间上的一元实函数.

导数定义与性质

在此先给出定义在$\mathbb{R}$的子集上的可微函数的定义, 并给出计算导数的基本法则.

[定义][导数]

令$D\subset \mathbb{R}$,称函数$f:D\rightarrow \mathbb{R}$在点$x_0\in D$可微, 若满足:$$f’(x_0):= \lim_{\small\begin{array}{c}
x \rightarrow x_0 \
x \in D\setminus {x_0}\end{array}}
\frac{f(x)-f(x_0)}{x-x_0}=
\lim_{\small\begin{array}{c}
h \rightarrow 0\
h \neq 0\
x_0 +h\in D\end{array}}
\frac{f(x_0 +h)-f(x_0)}{h}$$
存在. 有时也用符号$\frac{df}{dx}(x_0)$替代$f’(x_0)$, 称为函数$f$在点$x_0$处的\textbf{导数(微商)}.
若$\forall x \in D$, $f$皆可微, 则称函数$f$在$D$上是可微的.

序列与极限

这里我们快速的过一遍关于数列与级数的这一些基础的内容.这些内容在复数域 $\mathbb{C}$ 上都是成立的.

度量空间 $X$ 中的序列 ${ x_n }$ 称收敛的, 当 $\exists x \in X$, $\forall \varepsilon >0$, $\exists N\in \mathbb{N}_+ $, $d(x_n, x)<\varepsilon$. 我们说序列 ${ x_n }$ 收敛于 $x$.记为
$$\lim_{n\rightarrow\infty}x_{n} = x.$$
如果序列不收敛, 我们称其为发散的.

继续上一篇笔记, 接下来关注两个重要的拓扑性质——极限和连续.

连续

从拓扑结构出发刻画 连续

关于一般拓扑空间的连续性, 有多个等价定义和命题[1], 这里暂且只提最基本的一个.

从拓扑空间 $(X,\mathscr{T})$ 到拓扑空间 $(Y,\mathscr{U})$ 内的映射 $f$ 称为连续的, 当且仅当对于 $\mathscr{U}$ 中的每一个开集, 其在 $\mathscr{T}$ 中的原像为开集; 每一个闭集, 其在 $\mathscr{T}$ 中的原像为闭集.

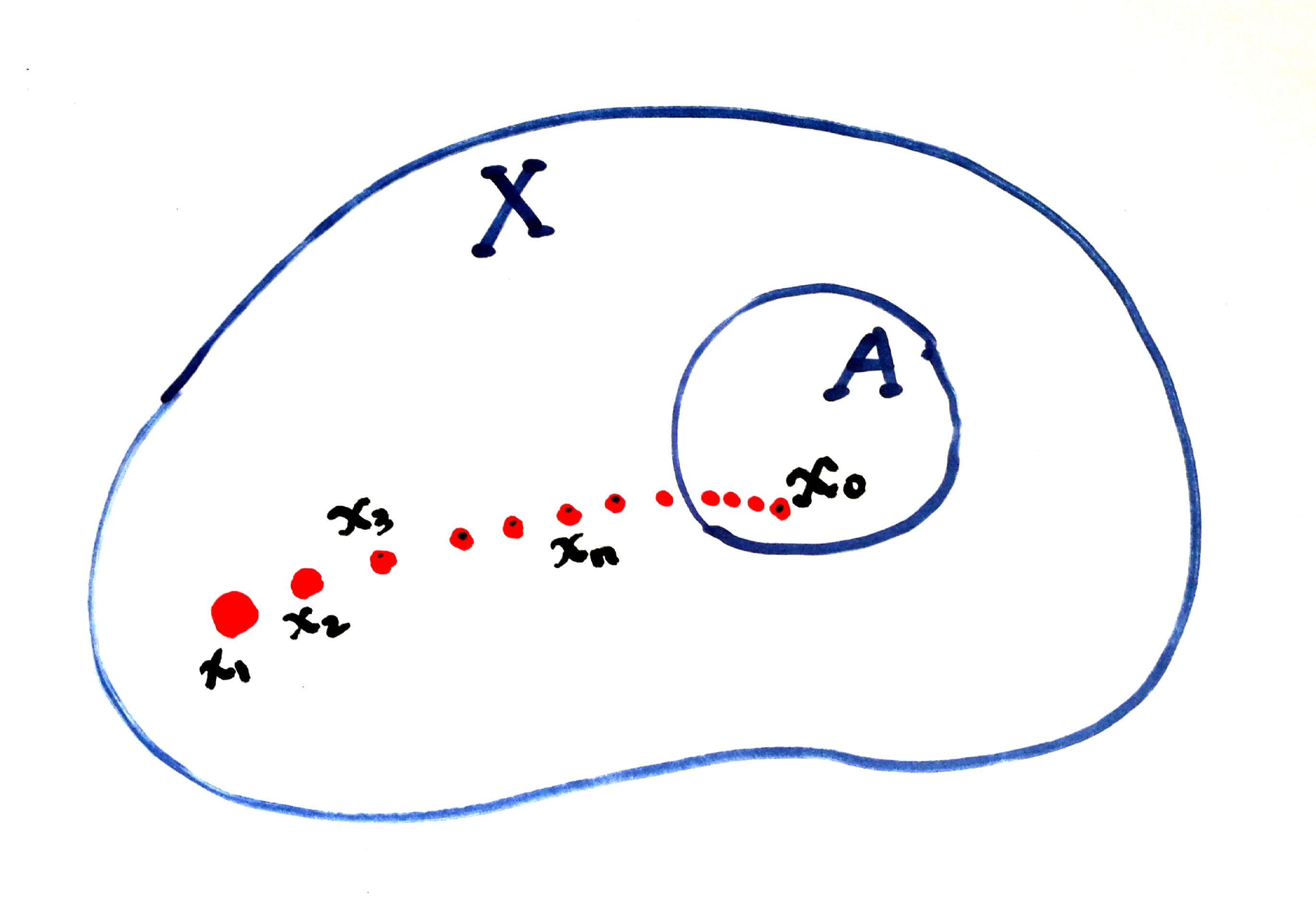这篇笔记主要内容是回顾 $\mathbb{R}^n$ 上的拓扑. 事实上,这里是要对由度量诱导的 $\mathbb{R}^n$ 的度量空间上的拓扑进行总结. 对于一般的拓扑空间(不依赖特定度量的性质)的拓扑性质, 更为详细的内容, 可以参考任意一本《点集拓扑学》或《一般拓扑学》之类的讲义. 事实上, 度量空间上的极限, 连续性, 和紧性都是空间拓扑性质的例子.

Mathematics links the abstract world of mental concepts to the real world of physical things without being located in completely in either.
**Ian Stewart** — Preface to second edition of *What is Mathematics?* by **Richard Courant** and **Herbert Robbins**, revised by **Ian Stewart** (1996).

说到微积分, 就要说到微积分所研究的主要对象——函数. 整个大千世界, 到处都是函数关系, 所以我们研究函数的目的不是为了纯理论的思辨, 而恰恰是我们对于理解世界的渴望, 对于各种经济利益的追求, 驱动着我们.