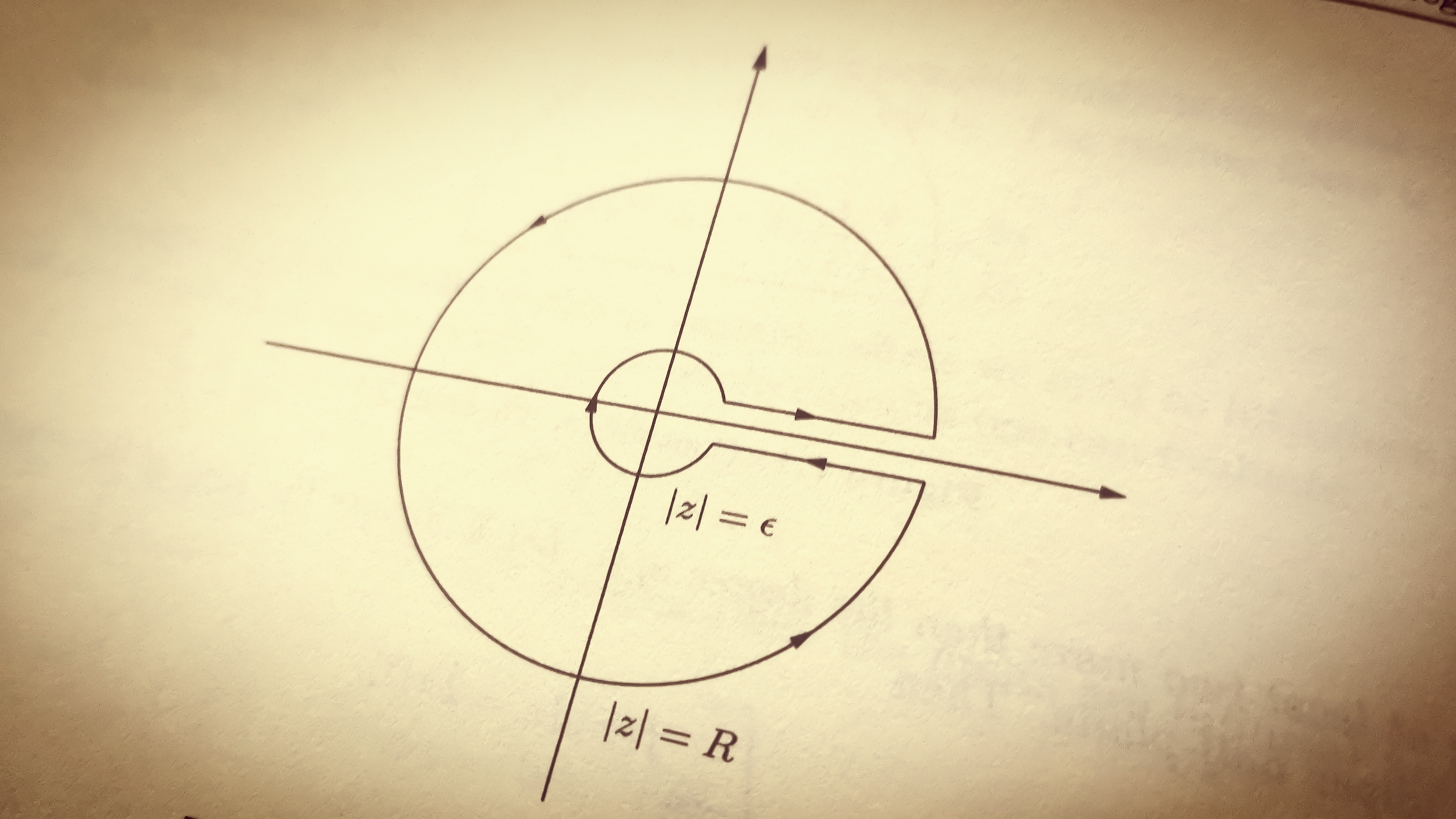
内容节选自 from J. Rotman’s Galois Theory - Appendix 1. 仅供学习时备忘使用.
Abelian Group. A group in which multiplication is commutative.
Alternating Group $A_n$. The subgroup of $S_n$ consisting of all the even permutations. it has order $\frac{1}{2}n!$.
Associativity. For all $x,y,z$, one has $(xy)z=x(yz)$. it follows that one does not need parentheses for any product of three or more factors.
Automorphism. An isomorphism of a group with itself.
Commutativity. For all $x,y$, one has $xy=yx$.