Review - $\mathbb{R}^{n}$ 上的拓扑(2)
继续上一篇笔记, 接下来关注两个重要的拓扑性质——极限和连续.
关于一般拓扑空间的连续性, 有多个等价定义和命题[1], 这里暂且只提最基本的一个.
从拓扑空间 $(X,\mathscr{T})$ 到拓扑空间 $(Y,\mathscr{U})$ 内的映射 $f$ 称为连续的, 当且仅当对于 $\mathscr{U}$ 中的每一个开集, 其在 $\mathscr{T}$ 中的原像为开集; 每一个闭集, 其在 $\mathscr{T}$ 中的原像为闭集.
Review - $\mathbb{R}^n$ 上的拓扑(1)
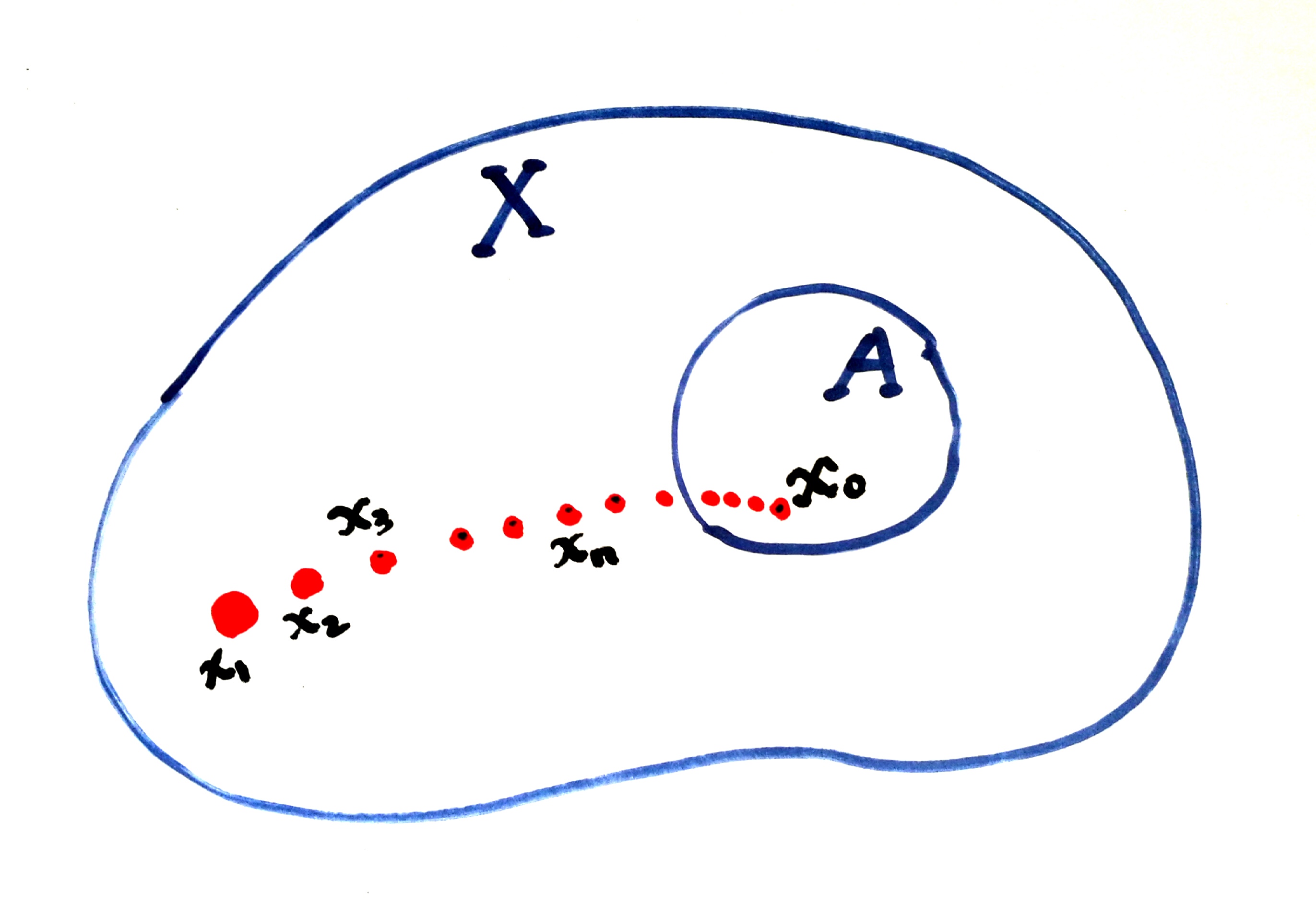这篇笔记主要内容是回顾 $\mathbb{R}^n$ 上的拓扑. 事实上,这里是要对由度量诱导的 $\mathbb{R}^n$ 的度量空间上的拓扑进行总结. 对于一般的拓扑空间(不依赖特定度量的性质)的拓扑性质, 更为详细的内容, 可以参考任意一本《点集拓扑学》或《一般拓扑学》之类的讲义. 事实上, 度量空间上的极限, 连续性, 和紧性都是空间拓扑性质的例子.
Mathematics links the abstract world of mental concepts to the real world of physical things without being located in completely in either.
**Ian Stewart** — Preface to second edition of *What is Mathematics?* by **Richard Courant** and **Herbert Robbins**, revised by **Ian Stewart** (1996).
说到微积分, 就要说到微积分所研究的主要对象——函数. 整个大千世界, 到处都是函数关系, 所以我们研究函数的目的不是为了纯理论的思辨, 而恰恰是我们对于理解世界的渴望, 对于各种经济利益的追求, 驱动着我们.
