逼近理论缘起

函数的最佳逼近问题起源于俄国数学家 P.L.切比雪夫. 1853 年, 当时切比雪夫正在研究关于将蒸汽引擎的线性运动转化为轮毂的圆周运动的联动装置的问题, 其中,他考虑了如下问题:

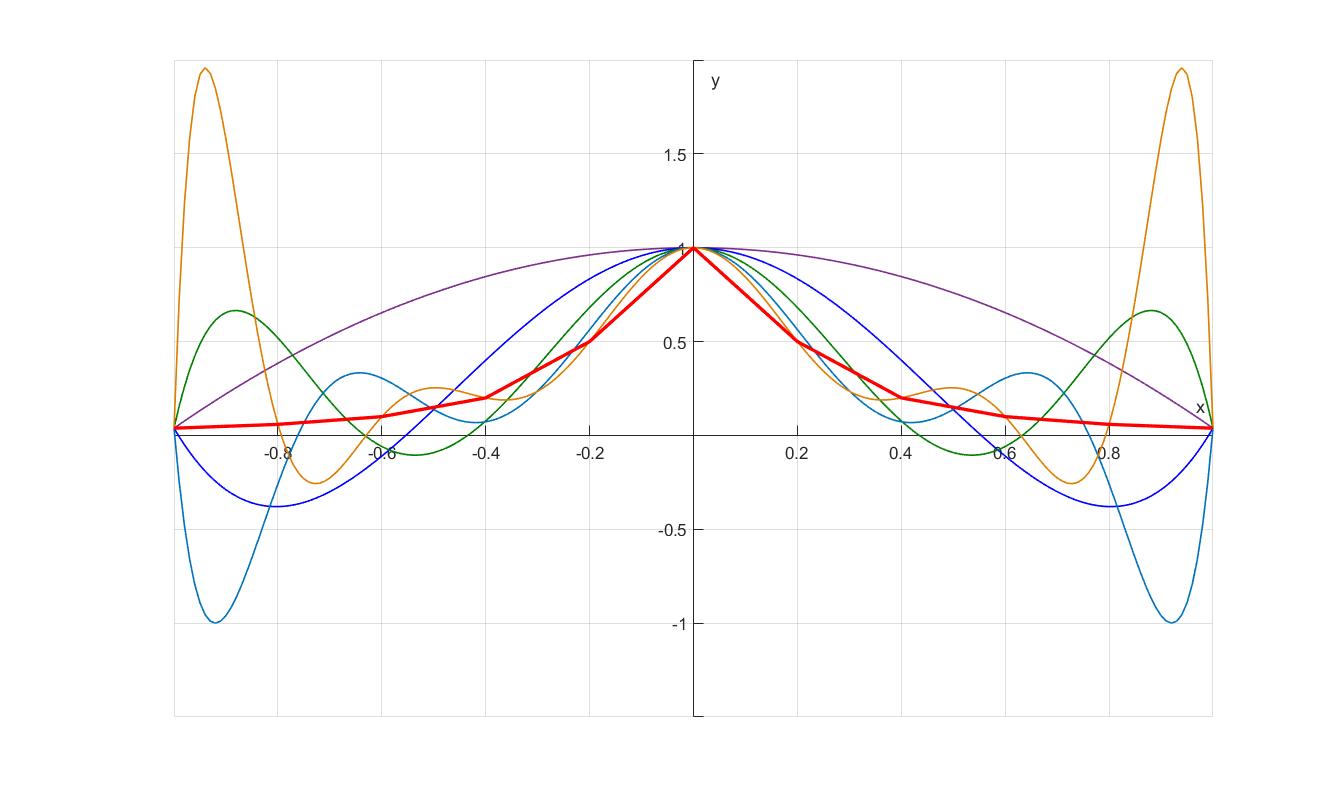
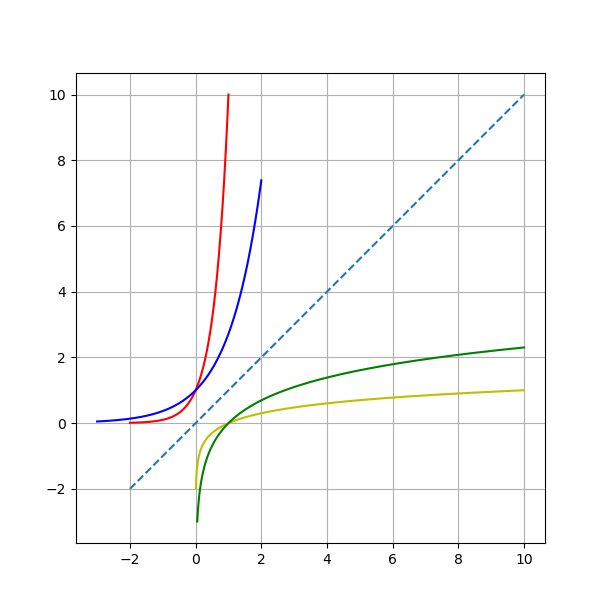
给出定义在闭区间 $[a, b]$ 上的连续函数 $f$, 以及正整数 $n$, 是否能用最高不超过 $n$ 次的多项式函数 $\sum_{k=0}^{n}a_k x^k$ 来近似表示函数 $f$, 在区间上的任意一点处的误差在可控制的范围内?

特别的, 我们是否能构造出多项式 $P(x)$ 使得误差 $\max_{a\leq x\leq b}|f(x)-P(X)|$ 最小?

【习题来源】数学分析：第七版.（俄罗斯）卓里奇著；李植译. 北京：高等教育出版社，2019.

1. 请证明:
   a) 如果 $f\in C(A)$ 且 $B \subset A$, 则 $f|_ B = C(B)$.
   
   b) 如果函数 $f: E_{1} \cup E_2 \rightarrow \mathbb{R}$, 满足 $f|_ {E_i} \in C(E_i), i = 1,2$, 则未必 $f\in C(E_1\cup E_2)$.
   
   c) 黎曼函数 $\mathscr{R}$ 以及它在有理数集上的限制 $\mathscr{R}|_ {\mathbb{Q}}$ 在集合 $\mathbb{Q}$ 的每一个非零的点间断, 并且所有的间断点都是可去间断点.

续上一篇 数学分析习题解-函数极限(1). 这一部分习题主要涉及无穷乘积.

7. 请证明:
   a) 级数 $\sum_{n=1}^{\infty}\ln a_n$ (其中 $a_n>0, n\in\mathbb{N}$) 收敛的充要条件是数列 $\{\prod_{n} = a_1\cdots a_n\}$ 有非零极限.
   
   b) 级数 $\sum_{n=1}^{\infty}\ln(1+a_n)$ (其中 $|a_n|<1$) 绝对收敛的充要条件是级数 $\sum_{n=1}^{\infty}a_n$ 绝对收敛.

【证明】
a) 若级数 $\sum_{n=1}^{\infty}\ln a_n$ 收敛, 则 $n\rightarrow\infty$ 时, $\sum_{k=1}^{n}\ln a_k = \ln(\Pi_n)$ 有极限. 由自然对数的性质立刻得知 $n\rightarrow\infty$ 时 $\Pi_n$ 趋于非零极限. 这些步骤都是可逆的, 必要性和充分性由此可以得到.

b) 由 $n\rightarrow\infty$ 时 $\ln (1+a_n)\sim a_n$ ($|a_n|<1$), 由前面的题 5 可知级数 $\sum_{n=1}^{\infty}|\ln(1+a_n)|$ 与级数 $\sum_{n=1}^{\infty}|a_n|$ 同时敛散. 故待证命题成立. Q.E.D.

【习题来源】数学分析：第七版.（俄罗斯）卓里奇著；李植译. 北京：高等教育出版社，2019.2

习题

1. a) 请证明: 在 $\mathbb{R}$ 上定义且满足以下要求的函数存在并且是唯一的:
   $$\begin{array}{c} f(1)=a\quad(a>0, a\neq 1),\\ f(x_1)\cdot f(x_2)=f(x_1+x_2),\\ x\rightarrow x_0, f(x)\rightarrow f(x_0). \end{array}$$
   b) 请证明: 在 $\mathbb{R_+}$ 上定义且满足以下要求的函数存在并且是唯一的:
   $$\begin{array}{c} f(1)=a\quad(a>0, a\neq 1),\\ f(x_1)\cdot f(x_2)=f(x_1+x_2),\\ x_0\in \mathbb{R_+}, \mathbb{R_+}\ni x\rightarrow x_0, f(x)\rightarrow f(x_0). \end{array}$$

这里, 我们利用实数理论以及极限理论来完整的定义指数函数, 对数函数以及幂函数的定义.

指数函数 $a^x$

设 $a>1$.

1. 对于 $n\in \mathbb{N}$, 归纳的定义 $a^1 = a, a^{n+1}=a^n\cdot a^1$, 这样我们就在 $\mathbb{N}$ 上定义了函数 $a^n$, 同时可以看出, 函数具有性质$a^m/a^n = a^{m-n}(m,n\in \mathbb{N}, m>n)$.
2. 由上面这个性质, 我们可以自然的定义 $a^0: = 1, a^{-n} = 1/a^n$. 于是, $a^n$ 的定义自然的拓展到了整数集 $\mathbb{Z}$ 上. $\forall n,m\in \mathbb{Z}, a^n\cdot a^m = a^{n+m}$.
3. 由实数理论, 我们知道 $\forall a> 0, n\in\mathbb{N},\exists \text{唯一的}x>0 (x^n = a)$. 用 $x = a^{1/n}$ 表示数 $a$ 的 $n$ 次方根. 这一记法保留了指数的加法规则. 于是我们可以进一步定义 $a^{m/n}(m,n\in\mathbb{N})$. 即对于 $r\in\mathbb{Q}$ 定义了 $a^r$.
4. 由归纳原理, 可以验证 $\forall x>0, y>0, n\in\mathbb{N}$ 时有 $(x< y)\Leftrightarrow(x^n< y^n)$ 和 $(x= y)\Leftrightarrow(x^n= y^n)$.
5. 由此我们可以证明有理指数的运算法则, 并得到 $\forall r_1,r_2\in \mathbb{Q}, a^{r_1}\cdot a^{r^2} = a^{r_1+r_2}$.
6. 由 4. 知 $r_1,r_2\in \mathbb{Q}, (r_1<r_2)\Leftrightarrow (a^{r_1}< a^{r^2})$.

【习题来源】数学分析：第七版.（俄罗斯）卓里奇著；李植译. 北京：高等教育出版社，2019.2

5. 请证明

• a) 当 $n\leqslant 2$ 时, 以下等式成立: $$\begin{array}{l} & 1+\frac{1}{1!}+\frac{1}{2!}+\cdots+\frac{1}{n!}+\frac{1}{n!n}\\ = & 3 - \frac{1}{1\cdot 2\cdot 2!}-\cdots -\frac{1}{(n-1)n\cdot n!}.\end{array}$$
• b) $$e = 3 - \sum_{n=0}^{\infty}\frac{1}{(n+1)(n+2)(n+2)!}.$$
• c) 为近似计算 $e$, 公式 $$1+\frac{1}{1!}+\frac{1}{2!}+\cdots+\frac{1}{n!}+\frac{1}{n!n}$$ 远好于原来的公式 $$1+\frac{1}{1!}+\frac{1}{2!}+\cdots+\frac{1}{n!}.$$

【习题来源】数学分析：第七版.（俄罗斯）卓里奇著；李植译. 北京：高等教育出版社，2019.2

4. 表达式 $$n_1 + \frac{1}{n_2 + \frac{1}{\begin{matrix} n_3 + \ddots & \\ & \frac{1}{n_{k-1}+\frac{1}{n_k}}\end{matrix}}},$$ 其中 $n_i\in\mathbb{N}$, 称为链式分数或有限连分数, 而表达式 $$n_1 + \frac{1}{n_2 + \frac{1}{n_3 + \ddots}}$$ 称为无穷连分数. 在一个连分数中去掉某个链开始的所有分数, 所得分数称为这个连分数的渐进分数. 无穷连分数的渐进分数序列极限是该无穷连分数的值.
   关于连分数的基本性质, 参考 Continued Fraction.
   请证明:

【习题来源】数学分析：第七版.（俄罗斯）卓里奇著；李植译. 北京：高等教育出版社，2019.2

习题

1. 请证明：数 $x\in \mathbb{R}$ 是有理数的充要条件是，它在任何 q-进制计数法中是循环的，即从某一位数开始，它由一组周期性重复的数码组成。

【证明】 充分性: 若 $x$ 在任意 q-进制下是循环的, 设循环节长度为 $k$, 显然 $n = q^k x - x$ 为有限小数, 即 $n$ 为有理数, 那么由有理数对四则运算的封闭性, 可知 $x$ 也是有理数.

这一部分主要集中讨论定义在闭区间上的一元实函数.

导数定义与性质

在此先给出定义在$\mathbb{R}$的子集上的可微函数的定义, 并给出计算导数的基本法则.

[定义][导数]

令$D\subset \mathbb{R}$,称函数$f:D\rightarrow \mathbb{R}$在点$x_0\in D$可微, 若满足: $$f’(x_0):= \lim_{\small\begin{array}{c} x \rightarrow x_0 \ x \in D\setminus {x_0}\end{array}} \frac{f(x)-f(x_0)}{x-x_0}= \lim_{\small\begin{array}{c} h \rightarrow 0\ h \neq 0\ x_0 +h\in D\end{array}} \frac{f(x_0 +h)-f(x_0)}{h}$$
存在. 有时也用符号$\frac{df}{dx}(x_0)$替代$f’(x_0)$, 称为函数$f$在点$x_0$处的\textbf{导数(微商)}.
若$\forall x \in D$, $f$皆可微, 则称函数$f$在$D$上是可微的.

序列与极限

这里我们快速的过一遍关于数列与级数的这一些基础的内容.这些内容在复数域 $\mathbb{C}$ 上都是成立的.

度量空间 $X$ 中的序列 ${ x_n }$ 称收敛的, 当 $\exists x \in X$, $\forall \varepsilon >0$, $\exists N\in \mathbb{N}_+$, $d(x_n, x)<\varepsilon$. 我们说序列 ${ x_n }$ 收敛于 $x$.记为
$$\lim_{n\rightarrow\infty}x_{n} = x.$$
如果序列不收敛, 我们称其为发散的.