平台：win64+anaconda

1. 查看已安装的库

打开 Anaconda Command Prompt ,在命令提示符窗口中输入以下命令：

1
2
3
4
5

pip list

# 或者

conda list

其中，pip list 只能查看库，而 conda list 则可以查看库以及库的版本

2. 如何安装或更新库

以安装 更新 scipy 为例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

pip install scipy
pip install scipy --upgrade

# 或者

conda install scipy
conda update scipy

# 更新所有库

conda update --all

# 更新 conda 自身

conda update conda

# 更新 anaconda 自身

conda update anaconda

话说, 在古希腊的神话传说里, 当一个神做了有利于人类的事, 为了激励他, 众神之王宙斯为了奖励他, 就会带他进入神殿里, 打开一扇窗, 让他看一眼宇宙的奥秘.

这是对一个传说中的神的奖励.

而今天, 一群科学家, 科学工作者, 这些凡人, 以凡人之心, 凡人之眼, 能真正去探究这个世界的奥秘, 这是对人类最大的奖励. 所以, 继续努力呗~

看到一道不难但是很有意思的综合性习题. 好吧, 事实上这是 2017 年中山大学研究生入学考试[高等代数]科目的最后一道题. 这道题将数学分析和高等代数的知识结合在一起, 值得一看. 也作为自己对相关知识点的一个小小的复习. 下面就是原题题目.

继续上一篇笔记, 接下来关注两个重要的拓扑性质——极限和连续.

连续

从拓扑结构出发刻画 连续

关于一般拓扑空间的连续性, 有多个等价定义和命题[1], 这里暂且只提最基本的一个.

从拓扑空间 $(X,\mathscr{T})$ 到拓扑空间 $(Y,\mathscr{U})$ 内的映射 $f$ 称为连续的, 当且仅当对于 $\mathscr{U}$ 中的每一个开集, 其在 $\mathscr{T}$ 中的原像为开集; 每一个闭集, 其在 $\mathscr{T}$ 中的原像为闭集.

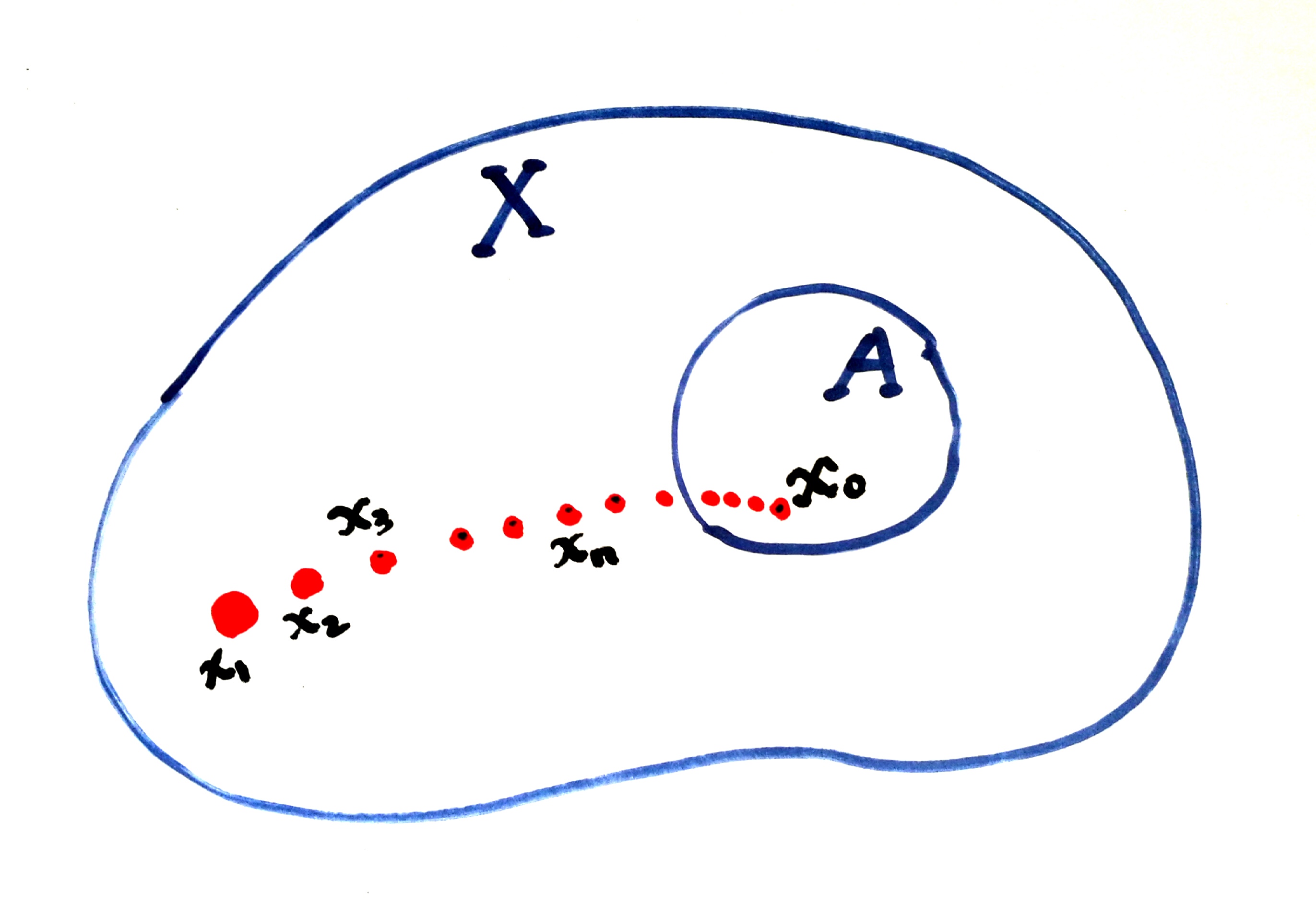这篇笔记主要内容是回顾 $\mathbb{R}^n$ 上的拓扑. 事实上,这里是要对由度量诱导的 $\mathbb{R}^n$ 的度量空间上的拓扑进行总结. 对于一般的拓扑空间(不依赖特定度量的性质)的拓扑性质, 更为详细的内容, 可以参考任意一本《点集拓扑学》或《一般拓扑学》之类的讲义. 事实上, 度量空间上的极限, 连续性, 和紧性都是空间拓扑性质的例子.

这是一些常用到的不等式,和大概的证明方法.部分方法很重要.