数学分析习题解-一致收敛性、函数项级数与函数族的基本运算(2)

【习题来源】数学分析：第七版.（俄罗斯）卓里奇著；李植译. 北京：高等教育出版社，2019.2

1. 请研究下列级数当实参数 $\alpha$ 取各种值时在集合 $E\subset\mathbb{R}$ 上的收敛性.
   a) $$\sum_{n=1}^{\infty}\frac{\cos nx}{n^\alpha};$$
   b) $$\sum_{n=1}^{\infty}\frac{\sin nx}{n^\alpha}.$$

【解】 显然, 上述两个级数在 $\alpha\leqslant 0$ 时不收敛, 在 $\alpha > 1$ 时绝对一致收敛(强函数检验法). 考虑在 $0< \alpha \leqslant 1$ 时的情况.

由以下关系式:
$$\begin{array}{c}\sum_{n=1}^{\infty}\cos nx=\frac{\cos\frac{n}{2}x \cdot \sin\frac{n+1}{2}x}{\sin\frac{x}{2}}\\
\sum_{n=1}^{\infty}\sin nx=\frac{\sin\frac{n}{2}x \cdot \sin\frac{n+1}{2}x}{\sin\frac{x}{2}}\end{array}$$
利用阿贝尔-狄利克雷判别法, 可知, 在 $\inf_{x\in E}|\sin\frac{x}{2}| > 0$ 的集合 $E$ 上, 以上两个级数一致收敛. 当 $x = 2\pi m , m \in \mathbb{Z}$, 级数 a) 收敛, 而 b) 则收敛到 0.

特别的, 只要集合 $E$ 的闭包 $\overline{E}$ 包含有 $2\pi m$, 由柯西准则可以判断出, 上述两个级数在 $E$ 上就不可能一致收敛. Q.E.D.

【幂级数的阿贝尔第二定理】 如果幂级数 $\sum_{n=1}^{\infty}c_n(z-z_0)^n$ 在某点 $\zeta\in \mathbb{C}$ 收敛, 则它在以 $z_0$, $\zeta$ 为端点的闭区间上一致收敛.

7. (阿贝尔第二定理的补充) 证明: 如果一个幂级数在其收敛圆边界上的某一个点收敛, 则它的和在这个圆中沿着任何不与圆周相切的方向趋于该点时均有极限.

【证明】 由于幂级数 $\sum_{n=1}^{\infty}c_n(z-z_0)^n$ 的收敛圆以 $z_0$ 为圆心, $r = 1/\overline{\lim_{n\rightarrow\infty}}\sqrt[n]{|c_n|}$ 为半径. 为简明记, 不失一般性的, 设 $z_0 = 0$, 收敛半径为 $1$. 再设幂级数在收敛圆边界上的一点 $\zeta = 1$ 处收敛 ( 对于一般形式的幂级数, 在边界上一点收敛, 设 $\widetilde{z}= (z - z_0)/(\widetilde{\zeta} - z_0)$, 令 $\widetilde{c}_n = c_n(\zeta - z_0)^n$ 即化为我们所做的简化假设的形式 $\sum \widetilde{c}_n \widetilde{z}^{n}$ ).

考察
$$\begin{equation}\label{eq:1}
\left|\sum_{k=n+1}^{m}c_k z^k\right|
\end{equation}$$
在 $z$ 沿着任意不与圆周相切方向趋于 $\zeta$ 时的情况.

由前设, 已知 $\sum{c_n}$ 收敛, 用 $s_n$ 表示其部分和 $\sum_{k=1}^{n}{c_n}$. 根据柯西准则, $\forall \varepsilon > 0, \exists N\in \mathbb{N}, \forall m, n >N \Rightarrow$
$$\begin{equation}\label{eq:2}|s_m-s_n| = \left|\sum_{k=n+1}^{m}c_k\right| < \varepsilon.\end{equation}$$

设 $A_k = s_k - s_n$. 对式 (\ref{eq:1}) 利用阿贝尔变换 有
$$\begin{array}{cl}
\left|\sum_{k=n+1}^{m}c_k z^k\right| &=& \left|\sum_{k=n+1}^{m}(A_k - A_{k-1}) z^k\right|\\
&=& \left|A_m z^m - A_n z^{n+1} + \sum_{k=n+1}^{m-1}A_k(z^k - z^{k+1})\right|\\
&\leqslant& \left|A_m z^m - A_n z^{n+1}\right| + \left|\sum_{k=n+1}^{m-1}A_k(z^k - z^{k+1})\right|\\
&\leqslant& \left|A_m - A_n \right||z^m| + \sum_{k=n+1}^{m-1}\left|A_k(z^k - z^{k+1})\right|\\
&\leqslant& \left|A_m - A_n \right||z^m| + |1-z|\sum_{k=n+1}^{m-1}\left|A_kz^k\right|
\end{array}$$
由式 (\ref{eq:2}) 以及 $|z|<1$, 对上式可以给出估计
$$\begin{equation}\label{eq:3}
\begin{array}{cl}
\left|\sum_{k=n+1}^{m}c_k z^k\right| &\leqslant& \varepsilon + \varepsilon\cdot|1-z|\sum_{k=n+1}^{m-1}\left|z^k\right|\\
&<& \varepsilon + \varepsilon\cdot\frac{|1-z|}{1-|z|}.\quad(\text{用到等比数列求和})
\end{array}
\end{equation}$$

现在关键之处在于对上式中 $\frac{|1-z|}{1-|z|}$ 部分进行估计.
我们考虑使用余弦定理
$$|\zeta-z|^2 + |\zeta - z_0|^2 -2|\zeta-z||\zeta-z_0|\cos\theta = |z-z_0|^2$$
即
$$\begin{equation}\label{eq:4}
|1-z|^2 + 1 -2|1-z|\cos\theta = |z|^2.
\end{equation}$$
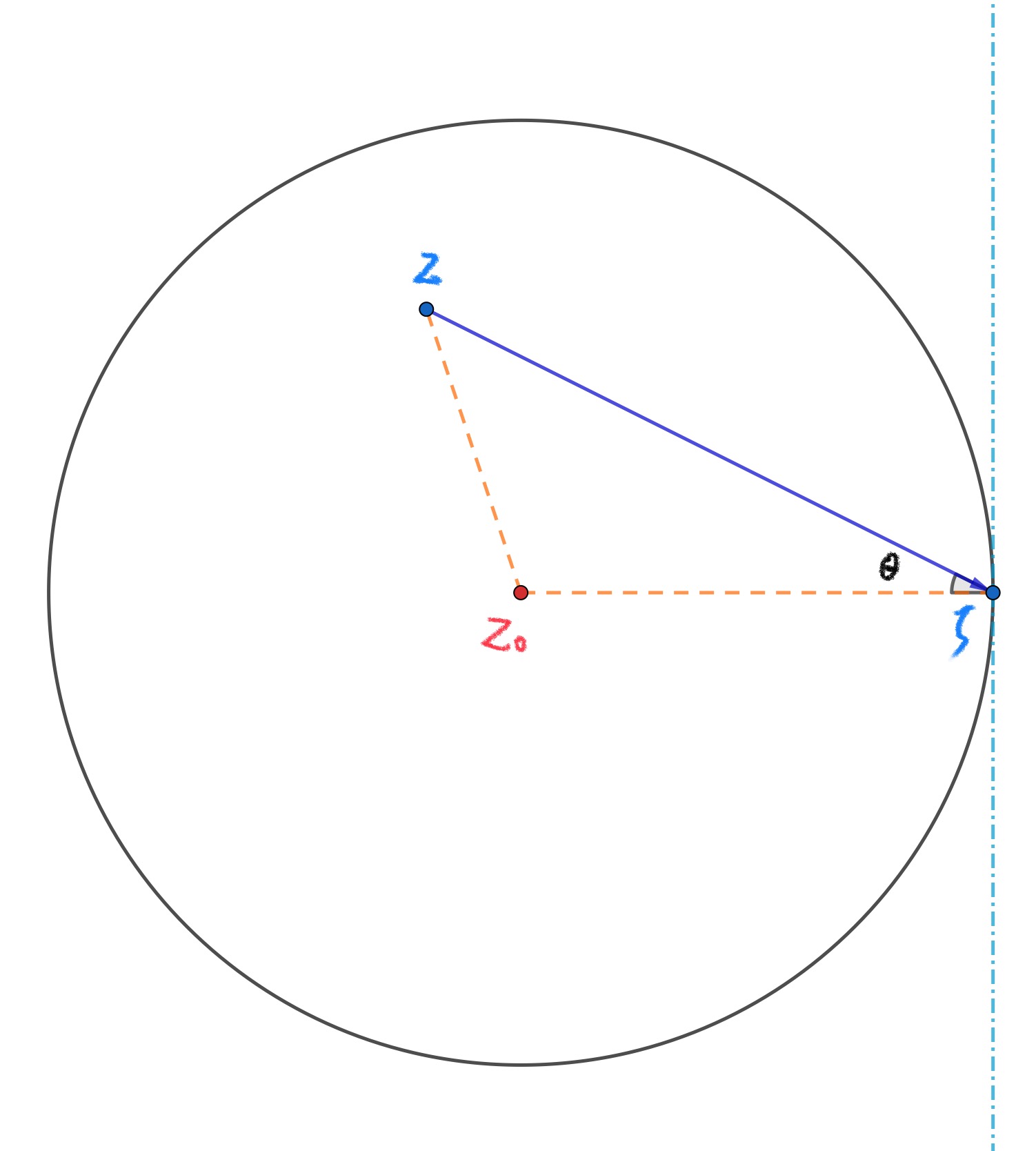
如下图, 这里 $\theta$ 是向量 $\overrightarrow{z\zeta}$ 与 向量 $\overrightarrow{z_0\zeta}$ 的夹角. $z$ 沿着不与圆周相切的方向趋于 $\zeta$ 即对应于 $\theta < \pi/2$ 的情况. 由式 (\ref{eq:4}) 得到
$$\frac{|1-z|}{1-|z|} = \frac{1+|z|}{2\cos\theta-|1-z|},$$
$z$ 趋于并足够接近 $1$ 时, 总有 $|1-\zeta|<\cos\theta$ (因为 $0 < \theta < 1$). 故而, 对式 (\ref{eq:3}) 进一步估计得到
$$\left|\sum_{k=n+1}^{m}c_k z^k\right| < \varepsilon + \varepsilon\cdot\frac{2}{\cos\theta}.$$

上式说明, 当$\theta < \pi/2$ (即不沿与圆周相切的方向)趋近于 $\zeta$ 时, 由级数收敛的柯西准则, 便得到我们要证明的结果.

事实上, 通过考察 $\left|\sum_{k=n+1}^{m}c_k z^k - \sum_{k=n+1}^{m}c_k\right|$ 还可以进一步得到该幂级数的和在这个圆中沿着任何不与圆周相切的方向趋于该点时的极限正是级数在 $\zeta$ 处的值 $\sum_{n=1}^{\infty}c_n$.