数学分析习题解-一致收敛性、函数项级数与函数族的基本运算(1)

【习题来源】数学分析：第七版.（俄罗斯）卓里奇著；李植译. 北京：高等教育出版社，2019.2

1. 以下函数序列是否一致收敛?
   a) $$f_n = \frac{\sin{nx}}{x^2}$$
   b) $$f_n = 2(n+1)x(1-x^2)^n$$
   c) $$f_n = \lim_{n\rightarrow\infty}(\cos m!\pi x)^{2n}$$

【解】 考察 $\Delta _n := \sup _{x\in E}|f(x) - f_n(x)|$ 在 $n\rightarrow \infty$ 时的情况即可. 容易得到 a) 一致收敛, b)、c) 不一致收敛. Q.E.D.

2. a) 函数 $f_n: X\rightarrow \mathbb{R}$ 由关系式 $f_n(x) = x^n$ 给出, 其中 $X = {x\in\mathbb{R}|x\geqslant 0}$. 证明: 该函数序列在任何区间 $[0,1-\delta]\subset [0,1]$ 上一致收敛, 而在 $[0,1]$ 上不一致收敛.
   
   b) 对于函数序列 $f_n(x) = x^n -x^{2n}$ 上述结论也成立.
   
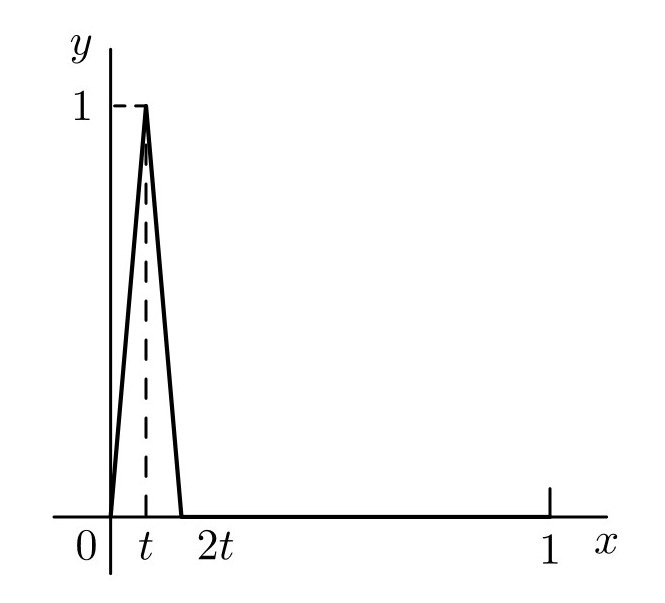
   c) 考虑定义在区间 $I = {x\in\mathbb{R}}$ 上的依赖于参数 $t\in[0,1]$ 的函数族 $f_t : I\rightarrow \mathbb{R}$. 其函数图像由下图给出:
   d) 研究函数族 $f_t(x) =\sin tx$ 当 $t\rightarrow 0$ 时的收敛性. 然后研究 $t\rightarrow \infty$ 的情况.
   e) 描述函数族 $f_t(x) = e^{-tx^{2}}$ 当$t\rightarrow \infty$ 时在任意固定集合 $E\subset \mathbb{R}$ 上的收敛性.

【证明】 a) 考察 $\Delta _n := \sup _{x\in E} |f(x) - f _n(x)|$ 在 $n\rightarrow \infty$ 时的情况. $\forall \delta >0 $
$$\Delta _n := \sup _{x\in [0,1-\delta]} |f(x) - f _n(x)|= (1-\delta)^n$$
在 $n\rightarrow \infty$ 时 $\Delta _n\rightarrow 0$. 故函数序列在任何区间 $[0,1-\delta]\subset [0,1]$ 上一致收敛.

而在 $[0,1]$ 区间上 $\Delta_n = 1$, 在 $n\rightarrow \infty$ 时 $\Delta _n$ 不 趋于 $0$. 故函数序列在任何区间 $[0,1]$ 上不一致收敛.

b) 同样的做法. 特别需要考虑的一点在于求 $\Delta_n$. 对 $f_n$ 关于 $x$ 求导, 可得 $x\in [0, \frac{1}{2}^{-1/n}]$ 上单调递增. 而我们知道数列的前有限项不影响其极限值. 以此为基础, 可知, 在 $[0,1-\delta]\subset [0,1]$ 上, $n\rightarrow \infty$ 时 $\Delta _n\rightarrow 0$.

c) 同上.

d) 当 $t\rightarrow 0$ 时, 函数族在 $\mathbb{R}$ 上不一致收敛, 但是在任意 $[a,b]\subset \mathbb{R}$ 上一致收敛. 显然, 函数在 $t\rightarrow \infty$ 时不收敛

e) 显然函数族在任意固定集合 $E\subset \mathbb{R}$ 上逐点收敛到 $f(x)=0$. 当 $0 \in E$ 时, 函数不一致收敛, 当 $0 \notin E$ 时, 函数一致收敛. Q.E.D.

4. a) 请验证, 如果一个函数族在一个集合上收敛(一致收敛), 则它在集合的任何子集中也收敛(一致收敛).
   
   b) 请证明, 如果函数族 $f_t: X\rightarrow \mathbb{R}$ 在集合 $E$ 和基 $\mathscr{B}$ 上收敛(一致收敛). 而 $g: X\rightarrow\mathbb{R}$ 是有界函数, 则函数族 $g\cdot f_t :X\rightarrow \mathbb{R}$ 在集合 $E$ 和基 $\mathscr{B}$ 上收敛(一致收敛).
   
   c) 请证明, 如果函数族 $f_t: X\rightarrow \mathbb{R}$, $g_t: X\rightarrow \mathbb{R}$在集合 $E$ 和基 $\mathscr{B}$ 上一致收敛, 则函数族 $\alpha f_t +\beta g_t$, ($\alpha, \beta \in \mathbb{R}$) 在集合 $E$ 和基 $\mathscr{B}$ 上一致收敛.

【证明】 由定义出发容易完成证明. Q.E.D.

5. a) 在证明柯西准则的充分条件时, 我们在 $T$ 的基 $\mathscr{B}$ 上取极限 $\lim_{\mathscr{B}}f_{t_1}(x) = f(x)$. 但是 $t_1\in B$, 而 $\mathscr{B}$ 是 $T$ 中的基, 而不是 $B$ 中的基. 我们能在保持 $t_1$ 属于 $B$ 的同时完成这个极限运算吗?
   
   b) 在证明函数族 $f_t$ 一致收敛的柯西准则时, 何处使用了 $\mathbb{R}$ 的完备性?
   
   c) 如果函数族 $f_t$ 中的所有函数都是常值函数, 则上述定理恰好给出函数 $\varphi: T\rightarrow \mathbb{R}$ 在 $T$ 的基 $\mathscr{B}$ 上极限存在的柯西准则.

【答】 a) 可以. 已知 $B\in \mathscr{B}$, 由基的定义, $\forall B_1 \in \mathscr{B}$, 有 $B\cap B_1 \in \mathscr{B}$.

b) $\forall x \in X$, $f_t$ 作为 $t$ 的函数在基 $\mathscr{B}$ 极限取极限时.

c) 由定义即得. Q.E.D.

6. 请证明: 如果闭区间 $I= \{ x\in \mathbb{R}|a\leqslant x\leqslant b \}$ 上的连续函数族 $f_t\in C(I,\mathbb{R})$ 在开区间 $(a,b)$ 上一致收敛, 则它在整个闭区间 $[a,b]$ 上一致收敛.

【证明】 注意到 $f_t\in C(I,\mathbb{R})$, 考虑函数族在两个端点处的收敛情况. 以 $b$ 为例, 由不等式
$$\begin{array}{cl}|f_{t_1}(b) - f_{t_2}(b)|&\leqslant& |f_{t_1}(b) - f_{t_1}(x)|\\
& &+|f_{t_1}(x)-f_{t_2}(x)|\\
& &+|f_{t_2}(x)-f_{t_2}(b)|\end{array}$$
进行估计, 由柯西准则即得在端点 $b$ 处收敛, 并给出了相应的基$\mathscr{B}$ 中的元素 $B_1$. 而函数族在开区间 $(a,b)$ 上一致收敛, 也可取到一个一致的 $B_0\in \mathscr{B}$. 只需取 $B:= B_0\cap B_1 \in\mathscr{B}$ 这样函数族就在在端点 $b$ 处一致收敛. Q.E.D.