指数函数, 对数函数以及幂函数的定义

这里, 我们利用实数理论以及极限理论来完整的定义指数函数, 对数函数以及幂函数的定义.

指数函数 $a^x$

设 $a>1$.

1. 对于 $n\in \mathbb{N}$, 归纳的定义 $a^1 = a, a^{n+1}=a^n\cdot a^1$, 这样我们就在 $\mathbb{N}$ 上定义了函数 $a^n$, 同时可以看出, 函数具有性质$a^m/a^n = a^{m-n}(m,n\in \mathbb{N}, m>n)$.
2. 由上面这个性质, 我们可以自然的定义 $a^0: = 1, a^{-n} = 1/a^n $. 于是, $a^n$ 的定义自然的拓展到了整数集 $\mathbb{Z}$ 上. $\forall n,m\in \mathbb{Z}, a^n\cdot a^m = a^{n+m}$.
3. 由实数理论, 我们知道 $\forall a> 0, n\in\mathbb{N},\exists \text{唯一的}x>0 (x^n = a)$. 用 $x = a^{1/n}$ 表示数 $a$ 的 $n$ 次方根. 这一记法保留了指数的加法规则. 于是我们可以进一步定义 $a^{m/n}(m,n\in\mathbb{N})$. 即对于 $r\in\mathbb{Q}$ 定义了 $a^r$.
4. 由归纳原理, 可以验证 $\forall x>0, y>0, n\in\mathbb{N}$ 时有 $(x< y)\Leftrightarrow(x^n< y^n)$ 和 $(x= y)\Leftrightarrow(x^n= y^n)$.
5. 由此我们可以证明有理指数的运算法则, 并得到 $\forall r_1,r_2\in \mathbb{Q}, a^{r_1}\cdot a^{r^2} = a^{r_1+r_2}$.
6. 由 4. 知 $r_1,r_2\in \mathbb{Q}, (r_1<r_2)\Leftrightarrow (a^{r_1}< a^{r^2})$.
7. 证明有理指数的极限性质, 即对于 $r_0\in \mathbb{Q}$, $$\lim_{\mathbb{Q}\ni r\rightarrow r_{0}}a^r = a^{r_0}.$$至此, 我们就定义了 $\mathbb{Q}$ 上具有以下性质的函数 $a^x$:
   • $a^1 = a>1$;
   • $a^{r_1}\cdot a^{r_2} = a^{r_1+r_2}$;
   • $(r_1<r_2)\Leftrightarrow (a^{r_1}< a^{r_2})$;
   • $\mathbb{Q}\ni r\rightarrow r_{0}$ 时 $a^r = a^{r_0}$.
8. 设 $x\in \mathbb{R}, s = \sup_{\mathbb{Q}\ni r< x}a^r, i = \inf_{\mathbb{Q}\ni r>x}a^r$. 可以证明 $s = i$.
9. 接着证明 $$a^x = \lim_{\mathbb{Q}\ni r\rightarrow x}a^r.$$于是我们就将指数函数的定义推广到了 $\mathbb{R}$ 上. 证明思想类似于作无理数的有理逼近.
10. 可以证明, 这个推广的定义继承了前面定义中所有的性质.

    【完备性公理】如果 $X$ 与 $Y$ 是 $\mathbb{R}$ 的非空子集, 且 $\forall x\in X, y\in Y$ 有 $x\leqslant y$, 则 $\exists c\in\mathbb{R}$ 使得 $\forall x\in X, y\in Y$, 有 $x\leqslant c\leqslant y$.

11. 最后, 我们指出, 函数 $x\mapsto a^x$ 的值域是 $\mathbb{R_+}$.
    事实上, $\forall y_0 \in \mathbb{R_+}$, 可以将定义域 $\mathbb{R}$ 分成两个集合: $A:=\{x\in\mathbb{R}|a^x<y_0\}$, $B:=\{x\in\mathbb{R}|a^x>y_0\}$. 显然 $A,B$ 都不是空集, 而由前述性质, (因$a>1$)有 $\forall x_1\in A, x_2\in B\Rightarrow (a^{x_1}< a^{x^2})$. 依据完备性公理, 存在 $x_0$ 使得 $\forall x_1\in A, x_2\in B$, 有 $x_1\leqslant x_0 \leqslant x_2$. 而利用反证法, 容易说明, $a^{x_0}= y_0$.
12. 前面我们均设 $a>1$, 而实际上对于 $0<a<1$, 可以重复类似过程, 只需注意 $r>0$ 时 $(r_1<r_2)\Leftrightarrow (a^{r_1}> a^{r_2})$. 于是在 $a>0, a\neq 1$, 我们在实数集上构造了函数 $x\mapsto a^x$, 其满足以下性质:
    - $a^1 = a>1$;
    - $a^{x_1}\cdot a^{x^2} = a^{x_1+x_2}$;
    - $a>1$ 时, $(x_1<x_2)\Leftrightarrow (a^{x_1}< a^{x_2})$;
    $0<a<1$ 时, $(x_1<x_2)\Leftrightarrow (a^{x_1}< a^{x_2})$;
    - 函数 $x\mapsto a^x$ 的值域是 $\mathbb{R_+}$.

【定义1】: 映射$$x\mapsto a^x$$称为以 $a$ 为底的指数函数. 有时也记为 $\exp_a x$.

对数函数 $\log_{a}(x)$

由指数函数的性质可知, 映射 $\exp_a x: \mathbb{R}\mapsto\mathbb{R_+}$ 是一个双射, 故其必存在逆映射.

【定义2】映射 $\exp_a x: \mathbb{R}\mapsto\mathbb{R_+}$ 的逆映射, 称为以 $a~(a>0, a\neq 1)$ 为底的对数函数, 记为
$$\log_{a}(x).$$
其中, 以 $a=e$ 为底的对数函数称为自然对数, 记为 $\ln: \mathbb{R}\mapsto\mathbb{R_+}$.

由以上定义以及指数函数的性质, 可以得到对数函数的性质:

• $\log_{a}a = 1$;
• $\log_{a}(y_1\cdot y_2) = \log_{a}y_1 +\log_{a}y_2$;
• 当 $\mathbb{R_+}\ni y\rightarrow y_0$ 时, $\log_{a}y\rightarrow\log_{a}y_0$;
• $a>1$ 时, $(y_1<y_2)\Leftrightarrow (\log_{a}y_1<\log_{a}y_2)$;
  $0<a<1$ 时, $(y_1<y_2)\Leftrightarrow (\log_{a}y_1>\log_{a}y_2)$
• 函数 $\log_{a}: \mathbb{R+}\mapsto\mathbb{R}$ 的值域为整个 $\mathbb{R}$.

对数函数还有一个性质:
$$\log_{a}b^\alpha = \alpha\log_{a}b.$$

【证明】 由对数的性质, $\log_{a}{(y_1\cdots y_n)} = \log_{a}y_1 +\cdots \log_{a}y_n.$ 当 $\alpha = n \in \mathbb{N}$ 时, $\log_{a}{b^n} = n\log_{a}b$.
又借由指数函数性质, 容易验证 $\log_{a}b^{-1}= -\log_{a}b$. 于是对于 $\alpha\in\mathbb{Z}$, 均有 $\log_{a}b^\alpha = \alpha\log_{a}b$ 成立. 进一步的, 由 $\log_{a}b = \alpha\log_{a}(b^{1/n})^n$, 容易得到对于 $\alpha\in\mathbb{Q}$, 命题也是成立的.
而由指数函数以及对数函数取极限的性质, 当 $\mathbb{Q}\ni r\rightarrow\alpha$ 时,
$$\lim_{\mathbb{Q}\ni r\rightarrow\alpha}\log_{a}b^r= \lim_{\mathbb{Q}\ni r\rightarrow\alpha}\log_{a}b^\alpha$$
进而可以证明得到命题. Q.E.D

由这一条性质我们可以反推出指数函数的另一条性质:

$$(a^\alpha)\beta = a^{\alpha\beta}.$$

幂函数 $x^a$

当我们定义 $1^\alpha = 1$.

【定义3】$\forall \alpha \in \mathbb{R}$, 定义函数 $x\mapsto x^\alpha$, 称为幂函数. 显然, 幂函数是指数函数和对数函数的复合函数.

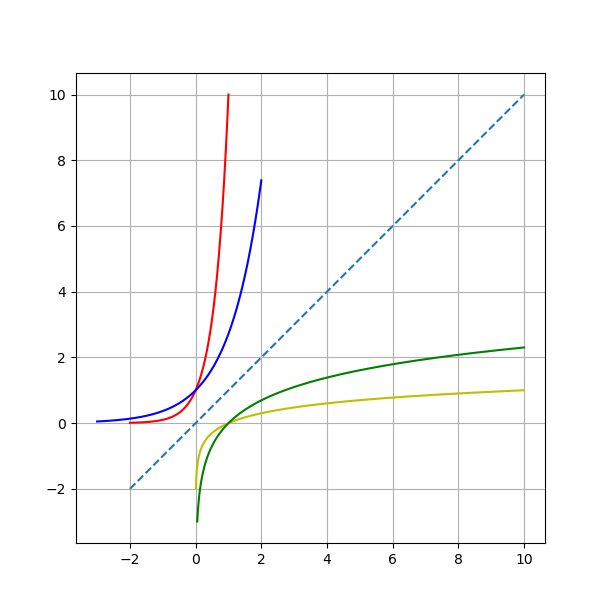
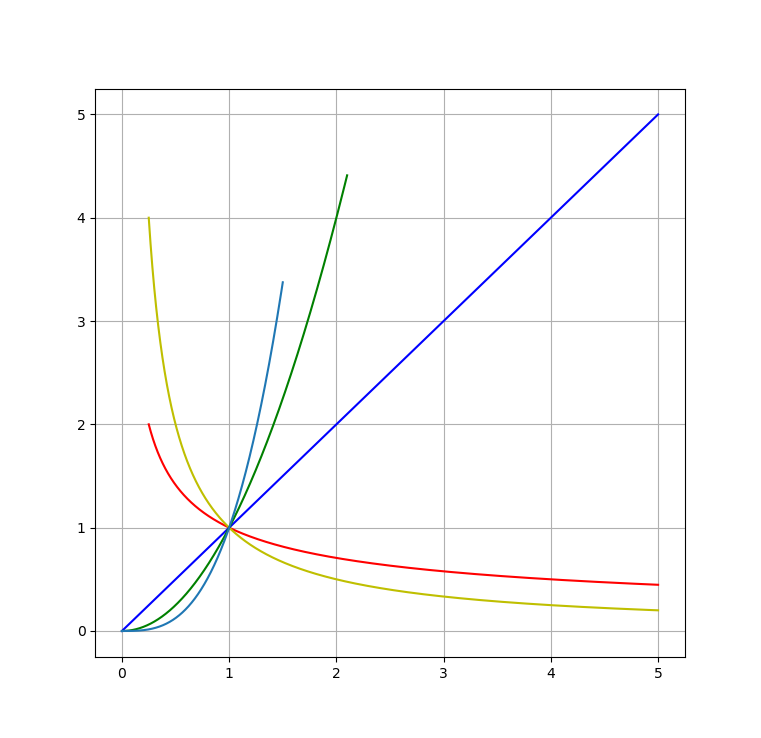
以下给出一些用 python 绘制的函数图像 直观感受一下.

全文参考: 数学分析：第七版.（俄罗斯）卓里奇著；李植译. 北京：高等教育出版社，2019.2