How to discover proofs?

本文节选自 Robert S.Strichartz《分析方法》（ *The Way of Analysis* ），由虎头微分同学从英文原版翻译而来。

这一节主要谈谈“证明”。 不仅仅是你在课本中读到的证明，还有在习题中， 你被要求做的“证明”练习。

什么是证明？你又应该如何去寻找一个证明？你应该如何书写证明？ 如果你在开始数学学习之旅前已经想过这些问题的话，那么你一定发现了，关于这些问题并没有简单的答案。虽然在数学界就此在一定程度上达成了某种共识，，但在关于“哪些才是重点”这件事上，不同的意见依然存在。

什么是“证明”？

原则上，“证明”是从假设到待证明命题的系列逻辑推理。而命题通常是一个蕴含式：“$P$ 和 $Q$ 蕴含（推出） $R$。” 此时，我们有两个假设 $P$ 和 $Q$，以及一个结论 $R$。所有在表达式 $P$，$Q$，$R$ 中出现的对象，都必须是事先定义好的。所以，阅读（或寻找）一个证明的第一步，就是确保你完全理解了假设和结论，并记住了其中所有对象的定义。在书本中，有些前提假设可能被隐藏在细节条文中，务必一字一句仔细阅读。

如何寻找一个“证明”？

一个证明中的推理过程，包括允许的逻辑推理原则和对公理（或是之前建立的定理）的应用。很多证明中常见的一种错误，就是在尚未验证某个定理所需要满足的相关条件时，就将该定理应用于证明之中。这很可能会导致错误证明（因为该定理可能并不适用），或者导致证明不完整（定理或许适用，但是证明中的某些关键想法需要我们先行验证定理所要求的条件）。还有一种常见错误，来源于使用了给定前提条件以外的假设。另外，比如说，定理要求你证明“对于所有的 $x$，都满足…”，而你只证明了“$x=2$时”的这一种情况，这种证明也是不对的。

当我们需要完成基于给定条件下的某个证明时，推荐按以下方式来做：

• 首先，我们可以先写下一个列表，_列出你所已知的东西_（比如：前提假设、关键对象的定义等），同时，_列出你需要证明的东西_（也就是结论，有些时候可以从定义去复述结论）；
• 然后，搜索可能将二者联系起来的那些定理。如果已知假设中，包含了你所知道的某一定理的假设条件，那么我们就很可能相应的推导出这一定理的结论——这是正向的方式；或者，你发现某一定理的结论和待证结论相同，那么该定理所需要满足的假设也就是你接下来要针对的新目标了——这是反向的方式。强烈建议同时利用正向、反向两种思维来寻求证明。

当然，很多时候，你想使用的定理和你想要应用这条定理的方式并不能完美对应。比如：正向思考中，你想要使用某个定理，但是应用该定理需要满足的条件并没有刚好在你前面所写的列表中，但是，（通过一点努力）你可以利用已知的东西推导出这些条件——这样，你便能建立一条假设条件之间的推理链，和一条通向结论的推理链。

如果你幸运的话，两个推理链条会在某一点相遇。于是你便可以将它们组合起来，形成一条从假设条件到结论的单向推理链，而这就是你所寻找的证明。（如图 1 所示）

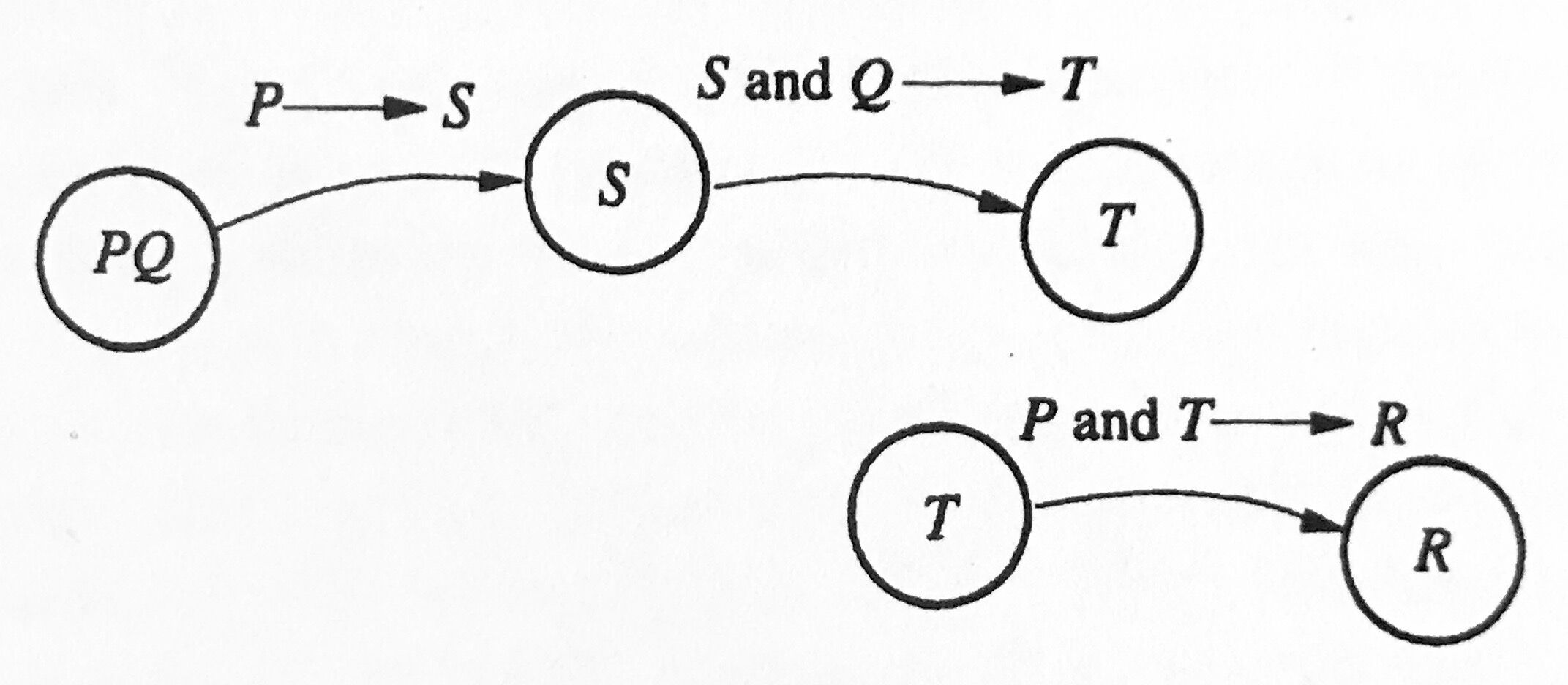
我们可以将这一简单的策略称为“嗅探（follow your nose）”。对于相对简单的问题，这一策略通常都会奏效。如果你遇到一些阻碍，这里有一个好技巧供你参考：一个好的问题，完成其证明通常需要充分利用其提供的每一个假设条件——所以，当你不知道接下来该往哪里走时，好好回顾一下“已知列表”，看看是否有哪些条件你还没有使用？然后再想办法用上它们（也就是寻找用到这些或能推出这些假设条件的定理）。

如果通过“嗅探”无法找到证明，那么也许你需要利用“构造法”来解决问题。也就是说，你需要引入一个新的，在前面的假设以及陈述的结论中未提及的对象。举例说，前提陈述中集中关注的是两个数 $x$ 和 $y$，那么也许你需要考虑平均值 $z = 1/2 ( x + y )$。 这只是一个简单的例子，但实际上，构造可以更加复杂精巧；这些精巧的构造往往需要天赋和创造力。在这方面并没有固定的套路，不过日常积累的经验将提供很大的启发。而构造的目的在于让更多的定理得以应用在解决问题上。若你发现一个定理与问题中所提到的对象有所关联，但并不完全能用起来的时候，这往往就是一个“需要构造”的提示了。

如何书写证明？

在你发现并验证一个成立的证明后，接下来就需要将证明写下来了。一般来说，书写证明有两种方式：按照发现证明的顺序，或将推理过程重整润色。以图 1 所示的推理链条为例，可能你首先注意到的是“$P$ 和 $T$ 推出 $R$”，然后是“$P$ 推出 $S$”，最后注意到“$S$ 和 $Q$ 推出 $T$”。

那么按照发现证明的顺序书写的证明是这样的：

**证明**： 我们要证明 $R$ 成立。但根据某某定理有 $P$ 和 $T$ 推出 $R$；而我们已知 $P$，只需证明 $T$ 成立就完成了证明。但我们注意到，根据某某定义 知 $P$ 能推出 $S$，同时根据前面的某某引理， $S$ 和 $Q$ 能推出 $T$。 综上，定理证明完毕。QED

或将推理过程按先后顺序重整，写下的证明是这样的：

**证明**： 假设 $P$ 与 $Q$成立。由某某定义，$P$ 推出 $S$，同时由前面的某某引理， $S$ 和 $Q$ 推出 $T$。于是我们同时有 $P$ 和 $T$ 成立。依据某某定理之假设，我们得到结论 $R$ 。QED

这种重整后的证明，好处在于容易跟随阅读。另一方面，第一种证明书写方式则体现了探索证明的过程，对于读者来说可能显得更合理。我们可以依据一些常识来决定选择何种书写方式（或者，我们可以适当调和一下，一部分证明以发现的顺序书写，同时在其中做适当的修饰，夹杂一些矫正顺序的叙述）。

有一件重要的事是我们必须抓住的，那就是证明中需要包含的细节数量。通常，存在一些非常简单的断言，它们可以合并叙述，又或者可以用一句“显然”一笔带过。毕竟，如果所有的简单断言都被写进证明，将使得证明过于冗长，以至于读者陷入“只见森林不见树木”的境地。另一方面，你不应该丢掉断言中的非初等部分，不该在推理中犯错。对一个写好的证明，终极的测试是其能否使读者信服。当然，这一点取决于读者！对于提交评分的作业来说，你最好在证明中包含足够的细节，以说服评分者你知晓并随时可以补足缺失的断言。对于课本中给出的证明，通常都会提供足够的细节以便你可以自己完成补全。

最后再提一句“反证法”（又叫“间接证明”，“矛盾推理”，或“逆否证明”）。其依据是广为认可的逻辑原则：“非 $Q$ 推出非 $P$, 与 $P$ 推出 $Q$ 等价”。所以，当证明命题“$P$ 推出 $Q$”时，可以先假设 $Q$ 是不成立的，并最终推导出矛盾。在这一方法中，你可能会在断言中同时用到假设条件 “$P$” 和 假定的 “非 $Q$”。当然，你最后会成功得到一个证明，但它可能会非常晦涩难懂。不过，按照我的经验，学生往往会在以下情况中滥用反证法：学生可能先假定 $Q$ 为假，然后通过某些断言推导出 $Q$，然后指出“$Q$”和“非 $Q$”是一对矛盾。然而事实上，这些推导原本可以写成“$P$ 推出 $Q$”的直接证明。一般来说，如果你的证明中出现了【“$Q$”和“非 $Q$”矛盾】这种情况，很大程度上就是犯了这个问题。当这种情况发生，请检查确认一下，在你的断言中，你是否正的需要用到“非 $Q$”这一假定。如果答案是“否”，你最好将定理改写为直接证明。

相比于“间接证明”，为什么我们往往更推崇“直接证明”呢？通常，“直接证明”会更具有“构造性”。如果结论是一个存在性陈述：“存在 $x$，使得…”，那么“直接证明”中可能会包含寻找 $x$ 的算法。相比于单纯说明“不存在这样的 $x$ 会导致矛盾”，这种证明给我们提供了更多地信息。