分析之【一元微分学】

这一部分主要集中讨论定义在闭区间上的一元实函数.

导数定义与性质

在此先给出定义在$\mathbb{R}$的子集上的可微函数的定义, 并给出计算导数的基本法则.

[定义][导数]

令$D\subset \mathbb{R}$,称函数$f:D\rightarrow \mathbb{R}$在点$x_0\in D$可微, 若满足:$$f’(x_0):= \lim_{\small\begin{array}{c}
x \rightarrow x_0 \
x \in D\setminus {x_0}\end{array}}
\frac{f(x)-f(x_0)}{x-x_0}=
\lim_{\small\begin{array}{c}
h \rightarrow 0\
h \neq 0\
x_0 +h\in D\end{array}}
\frac{f(x_0 +h)-f(x_0)}{h}$$
存在. 有时也用符号$\frac{df}{dx}(x_0)$替代$f’(x_0)$, 称为函数$f$在点$x_0$处的\textbf{导数(微商)}.
若$\forall x \in D$, $f$皆可微, 则称函数$f$在$D$上是可微的.

上面的定义中可以考虑单侧极限, 进而得到单侧导数的定义.函数在一点未必有定义但可以在这一点处有导数.

导数的几何意义是明显的.考虑函数$f$在$x_0$附近的图像, 经过图像上的两点$(x_0,f(x_0)),(x,f(x))$,可以做一条割线.$x\rightarrow x_0$时, 若$f$在点$x_0$处可导 , 则这条割线的极限位置, 就是$f$在$x_0$处的切线,斜率为$f’(x_0)$.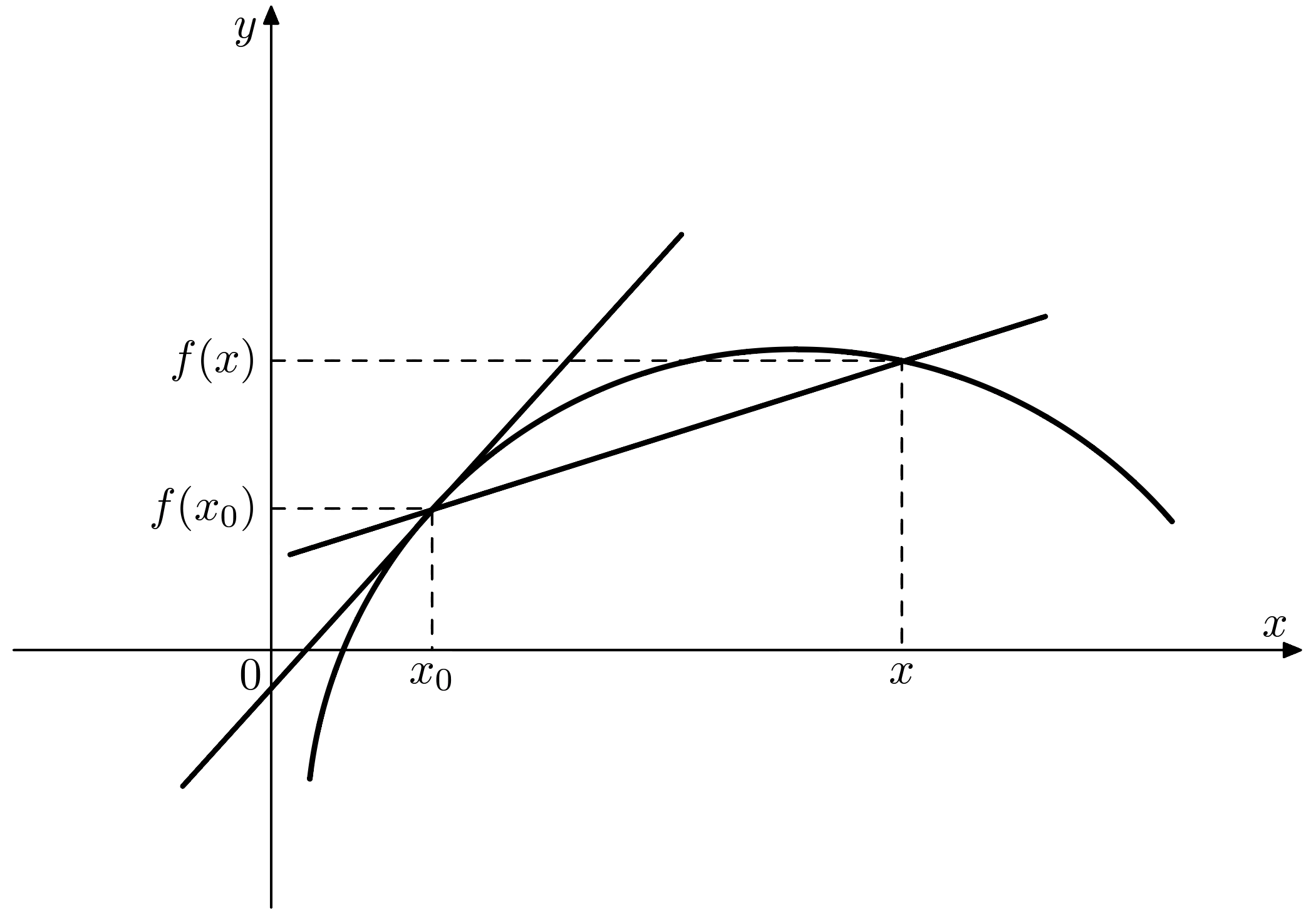

其实切线可以视为函数$f$在$x_0$处的线性近似,从这里,我们引入微分学的主要工具之一,有限增量公式, 也就是微分的概念.

[定义][微分]

设$f$是在$x_0$附近有定义的函数,如果存在常数$A$使得$$f(x)=f(x_0)+A(x-x_0)+o(x-x_0),\quad x\rightarrow x_0,$$
其中$o(x-x_0)$为无穷小量.则称$f$在$x_0$处可微, $x_0$处的线性映射$x\longmapsto Ax$称为$f$在$x_0$处的微分,记为$df(x_0)$.

导数和微分的关系,表现为有限增量公式,即

[定理][有限增量公式]

设$f$在$x_0$附近有定义,$f$在$x_0$处可导,当且仅当$f$在$x_0$处可微. 并且有$A=f’(x_0)$,即
$$\Delta y= f(x)-f(x_0)= f’(x_0)\Delta x +o(\Delta),\quad x\rightarrow x_0.$$
上式也可以写成另一个形式
$$\Delta y = f’(x_0)\Delta x+\omega(x)\Delta x$$
其中函数$\omega(x)$满足$\lim\limits_{x\rightarrow x_0}\omega(x)=\omega(x_0)=0$.

由此可立得

[定理]
若函数$f:D\rightarrow \mathbb{R}$在$x_0 \in D$上可微,则函数$f$在$x_0$点连续.

以上命题得逆命题并不成立. 在整个定义域上处处连续单数处处不可微的一个例子是 Weiestrass 给出的函数.

由极限的运算和导数的定义, 容易得到导数的运算性质:

设函数$f, g: D\rightarrow \mathbb{R}$, 均在点$x\in D$可微,则$f+g$,$fg$,$f/g$均在$x$点可微, 且
- $(f+g)’(x)=f’(x)+g’(x)$;
- $(fg)’(x)=f’(x)g(x)+f(x)g’(x)$;
- 若$g(x)\neq 0$, $\left(\frac{f}{g}\right)’ (x) = \frac{g(x)f’(x)-g’(x)f(x)}{g^2(x)}$.

下面是重要的\textbf{链式法则}.用导数的定义容易证明.

[定理][链式法则]

设$f:D_1 \rightarrow \mathbb{R}$在点$x\in D_1$可微, 同时$f(D_1)\subset D_2$. 再设$g:D_2 \rightarrow \mathbb{R}$,在点$y:=f(x)$可微. 那么两个函数的复合函数$g\circ f$在$x$可微. 且$$(g\circ f)’=g’(f(x))f’(x).$$

接下来是另一个重要的结果, 使得我们在知道一个函数的导数的情况下, 可以计算这个函数的反函数的导数. 当然, 反函数的存在是有条件的, 为此先给出函数单调的定义.

[定义][单调]

我们称函数$f:I\rightarrow \mathbb{R}$($I$为区间)\textbf{单调增加(减少)},当$\forall x_1, x_2 \in I, x_1 < x_2$时, 有$f(x_1)\leqslant(\geqslant)f(x_2)$. 称函数$f:I\rightarrow \mathbb{R}$($I$为区间)\textbf{严格单调增加(减少)},当$\forall x_1, x_2 \in I, x_1 < x_2$时, 有$f(x_1)< (>) f(x_2)$.

于是关于反函数存在及求导规则, 有以下结果:

[定理][反函数求导法则]

令$I\subset \mathbb{R}$为一开区间,而函数$f:I\rightarrow \mathbb{R}$是严格单调递增(递减)的,那么,存在连续函数$\varphi:f(I)\rightarrow \mathbb{R}$, 其满足$\forall x \in I, \varphi\circ f(x)=x$, $\forall y \in f(I), f\circ \varphi(y)=y$. $\varphi$称之为\textbf{函数$f$在区间$I$上的反函数}, 用符号$f^{-1}$表示.若函数$f:I\rightarrow \mathbb{R}$在$x \in I$上可微, 并且$f’(x)\neq 0$, 那么$\varphi$在点$y:=f(x)$可微, 并且
$$\varphi’(y)=\frac{1}{f’(x)}=\frac{1}{f’(\varphi(y))}.$$

接下来给出高阶导数的定义.

[定义]

如果函数$f:D\rightarrow \mathbb{R}$是可微的, 而其导函数$f’$在$D$上又是可微的, 则记$f’$的导函数数为$f’’$, 称为$f$的二阶导数. 如此继续定义, 可以得到
$$f,f’’,f^{(3)},\cdots,f^{(n)}$$
这一系列函数, 每一个都是前一个的导函数. $f^{(n)}$称为函数$f$的$n$阶导函数. 也可以用符号$\frac{d^{n}f}{dx^{n}}$来表示.

另外我们用符号$C^k(D,\mathbb{R})$表示由$D$上的$k$-重连续可微的实函数构成的向量空间. 定义$C^\infty(D,\mathbb{R})=C^\infty(D):= \bigcap_{k\in\mathbb{N}}C^k(D)$为$D$上无限阶连续可微的实函数构成的向量空间.

对于高阶导数的计算, 一个主要的工具就是莱布尼茨(Leibniz)公式:
\begin{array}{c}
(uv)^{(n)} & = & C_{n}^{0}u^{0}v^{n}+C_{n}^{1}u’v^{(n-1)}+C_{n}^{2}u’’v^{(n-2)}+\cdots+C_{n}^{n}u^{(n)}v^{(0)}\\
\quad & = & \sum_{k=0}^{n}C_{n}^{k}u^{(k)}v^{(n-k)}.
\end{array}

这里举一个数学分析中的重要而且有趣的例子. 我们知道函数$e^x$是$C^\infty(\mathbb{R})$的, 可以借此构造一个不那么平凡的$C^\infty(\mathbb{R})$函数的例子,其中的辅助函数,在解决一些问题时有用.

[举例]

定义函数
$$f(x):=\begin{cases} e^{-\frac{1}{x^2}},\quad x\neq 0, \ 0,\quad x=0, \end{cases}.$$
显然这是一个$\mathbb{R}$上的非常值函数.而事实上利用链式法则和数学归纳法,可以证明这个函数在$x=0$处的任意阶导数都等于$0$.

可微函数性质

关于可微函数典型的一些性质, 我们从微分中值定理开始介绍, 并给出一些应用. 还有重要的泰勒公式. 这些内容构成了微分学的核心部分.

中值定理

先引入局部极大值(极小值)的定义

[定义]

设$f$是定义在度量空间$X$上的实值函数,称$f$在点$p\in X$取得**局部极大值(极小值),若$\exists \delta >0$,当$d(p,q)<\delta$而且$q\in X$时, 有$f(q)\leqslant (\geqslant)f(p)$.

[定理][Taylor]

设函数$f:(a,b)\rightarrow \mathbb{R}$在$x_0\in (a,b)$取得局部极大(小)值, 而$f$在$x_0$处可微, 则$f’(x_0)=0$.

我们常见的中值定理有三个, Rolle, Lagrange, Cauchy,这三个中值定理一个比一个更一般.

[定理][Cauchy 中值定理]

连续实函数$f,g:[a,b]\rightarrow \mathbb{R}$, 它们在$(a,b)$中可微(端点不要求), 则$\exists \xi \in (a,b)$, 使得
$$[g(b)-g(a)]f’(\xi)=[f(b)-f(a)]g’(\xi).$$

若在上面的定理中取$g(x)=x$, 则得到:

[定理][Lagrange 中值定理]

连续实函数$f:[a,b]\rightarrow \mathbb{R}$, 其在$(a,b)$中可微(端点不要求), 则$\exists \xi \in (a,b)$, 使得
$$\frac{f(b)-f(a)}{b-a}=f’(\xi).$$

进一步的, 若函数$f$在两端点的函数值相等,即$f(a)=f(b)$,则有以下定理:

[定理][Rolle 中值定理]

连续实函数$f:[a,b]\rightarrow \mathbb{R}$, 它们在$(a,b)$中可微(端点不要求), 同时$f(a)=f(b)$,则$\exists \xi \in (a,b)$, 使得
$$f’(\xi)=0.$$

一个函数可以有处处存在(但可能在某些点间断的)导函数, 但并非每个函数都是某一个函数的导函数.作为中值定理的一个应用, 我们可以得到关于导函数的两个重要的基本定理.

[定理][达布(Darboux)定理]

设$f$在区间$I$上可微, 则$f’$具有介值性.

[定理][导函数极限定理]

设函数$f$在点$a$的某邻域$U(a)$内连续, 在$U(a)\setminus{a}$内可导. 若导函数$f’$在$a$存在极限,则函数$f$在$a$点可导, 且$f’(x)$在$a$连续.

由以上定理推论得知: 若函数$f$在区间$I$上可微, 那么其导函数$f’$不存在第一类间断点.

应用Cauchy中值定理, 还可以证明得到一个求极限很有用的定理:

[定理][洛必达(L’Hospital)法则]

设$f,g$在$(a,b)$内可导($-\infty\leqslant a < b\leqslant+\infty$), 且$\forall x\in (a,b),g’(x)\neq 0$.
再设
$$\lim_{x\rightarrow a+}f(x)=\lim_{x\rightarrow a+}g(x)=0,$$
或是
$$\lim_{x\rightarrow a+}g(x)=\infty,$$
而,极限
$$\lim_{x\rightarrow a+}\frac{f’(x)}{g’(x)}=A$$
存在(或为$\infty$), 那么
$$\lim_{x\rightarrow a+}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a+}\frac{f’(x)}{g’(x)}=A.$$

中值定理的应用是很丰富的, 这里再给出几个有意思的结果.下面这个结果由 Lagrange 中值定理导出.

[引理1]

设函数$f:[a,b]\rightarrow \mathbb{R}$, 在$[a,b]$上连续, 在$(a,b)$中可微. 若$\forall x\in(a,b)$,有$\mu\leqslant f’(x)\leqslant\eta$, 那么有结论: 对于$a\leqslant x_1\leqslant x_2\leqslant b$, 有
$$\mu(x_2-x_1)\leqslant f(x_2)-f(x_1)\leqslant\eta(x_2-x_1).$$

特别的, 我们进一步得到判断可微函数单调性的简单方法:

[引理2]

设函数$f:(a,b)\rightarrow \mathbb{R}$是可微的, 若$\forall x\in (a,b), f(x)\geqslant (\leqslant)0$, 那么$f$在$(a,b)$上单调增加(单调减少).

若函数在点$x_0$处有$f’(x_0)=0$, 且其\textbf{二阶可微}, 则有以下结果, 可用于判断$x_0$是否是函数的局部极大值(局部极小值):

[定理]

设函数$f:(a,b)\rightarrow \mathbb{R}$是二阶可微的. 对于点$x_0\in(a,b)$, 若有
$$f’(x_0)=0, f’’(x_0)<(>)0$$
则$f$在$x_0$处取到严格的局部极大值(局部极小值).

由(\ref{cor:1})还可得到以下结果:

[引理3]

设函数$f_1,f_2:[a,b]\rightarrow \mathbb{R}$, 均在$[a,b]$上连续, 在$(a,b)$中可微.若有$f_1(a)=f_2(a)$,$\forall x\in (a,b), f_1’(x)\leqslant f_2’(x)$, 则$\forall x\in (a,b), f_1(x)\leqslant f_2(x)$.

泰勒公式

前面谈到研究函数性态的工具, 函数$f$在定义域上一点$x_0$处可微, 那么在$x_0$的近旁可以用一个线性函数去近似. 若一个函数高阶可微, 在局部我们可以考虑用多项式来逼近, 以方便研究函数在局部的性态.这就是可以称为\textbf{微分学顶峰}的\textbf{Taylor 展开公式(定理)}.

[定理][(带Peano余项的)Taylor 公式]

若函数$f$在$x_0$处$n$阶可微,则有
$$f(x)= \sum_{k=0}^{n}\frac{1}{k!}f^{(k)}(x_0)(x-x_0)^k +o((x-x_0)^n), \quad (x\rightarrow x_0).$$
其中$$R_n(x):= f(x)-\sum_{k=0}^{n}f^{(k)}(x_0)(x-x_0)^k = o((x-x_0)^n)$$称为\textbf{Peano余项}.

上述定理中, 余项$R_n(x)$是一个无穷小量. 实际应用中,我们往往需要对逼近的误差进行更精确的估计, 这要求函数拥有更强一点的条件. 以下结果又称为Taylor 中值定理.

[定理][Taylor 中值定理]

设函数$f$在$(a,b)$上有直到$n+1$阶的导数,对于$x_0, x\in(a,b)$, 存在点$\xi,\zeta\in(x_0,x)$(或者$\xi,\zeta\in(x_0,x)$, 这取决于$x_0, x$的大小关系), 有
$$f(x)= \sum_{k=0}^{n}\frac{1}{k!}f^{(k)}(x_0)(x-x_0)^k + \frac{1}{(n+1)!}f^{(n+1)}(\xi)(x-x_0)^{n+1}$$
以及
$$f(x)= \sum_{k=0}^{n}\frac{1}{k!}f^{(k)}(x_0)(x-x_0)^k + \frac{1}{n!}f^{(n+1)}(\zeta)(x-\zeta)^n(x-x_0).$$
这两个展开式的余项分别称为Lagrange余项与Cauchy余项.

应用:关于微分方程的一些结论

这一节的主题是微分学, 作为这一主题的延伸应用, 最后我们谈论一点微分方程.

微分方程是数学方程的一种,用来描述某一类函数与其导数之间的关系.微分方程的解是一个符合方程的函数.(在初等数学的代数方程里,其解是常数值.)微分方程的应用十分广泛,可以解决许多与导数有关的问题,比如:物理中许多涉及变力的运动学、动力学问题;如空气的阻力为速度函数的落体运动等问题. 此外,微分方程在化学、工程学、经济学和人口统计等领域都有应用.

下面给出几个关于微分方程的结论.

我们用$a\leqslant x\leqslant b$,$\alpha\leqslant y \leqslant\beta$表示平面上的矩形区域$R$,设$\phi$为定义在$R$上的实函数.所谓初值问题
$$y’=\phi(x,y),\quad y(a)=c$$
的解,是$[a,b]$上的一个函数$f$,其满足$f(a)=c$,$\alpha\leqslant f(x)\leqslant \beta$,并且$$f’(x)=\phi(x, f(x)),\quad (a\leqslant x\leqslant b)$$.

[定理]

设函数$\phi:\mathbb{R}\rightarrow\mathbb{R}$是Lipschitz连续的, 那么初值问题最多只有一个解.

\begin{proof}
为证明这个命题,我们先证明一个引理:

[引理]

可微函数$F:[a,b]\rightarrow \mathbb{R}$满足$\forall x\in[a,b]$,$|F’(x)|\leqslant A|F(x)|$, $A>0$为一个常数. 若$\exists x_0\in [a,b], F(x_0)=0$,则在$[a,b]$上$F\equiv 0$.

定义$\delta:=\frac{1}{2A}$.在$I:=[a,b]\cap[x_0-\delta,x_0+\delta]$中取点$x_1$,满足$$|F(x_1)|=\sup_{x\in I}|F(x)|.$$
由$F$的连续性,这样的$x_1$是取得到的.由推论(\ref{cor:1}),有
\begin{array}{c}
|F(x_1)|=|F(x_1)-F(x_0)|\leqslant |x_1-x_0|\sup_{\xi\in I}|F’(x)|\\
\leqslant A\sup_{\xi\in I}|F(x)||x_1-x_0|\leqslant A\delta|F(x_1)|=\frac{1}{2}|F(x_1)|.
\end{array}
这说明$F(x_1)=0$,进而有$$F(x)=0~(\forall x\in I).$$
于是我们便证明了这样一件事:存在$\delta>0$, 当$F(x_0)=0$,则$\forall x\in [a,b]\cap[x_0-\delta,x_0+\delta], F(x)=0$.
如果函数$F$在$[a,b]$上不完全等于$0$,那么总是存在或最小的$\xi_1\in(a,b],F(\xi_1)=0$,或是最大的$\xi_2\in[a,b), F(\xi_2)=0$.而这与我们前面证明的事情是矛盾的.于是引理便得到了证实.

现在假设$f_1,f_2$均为初值问题的解,满足$f_1(a)=f_2(a)=c$. 那么函数$F=f_1-f_2$满足
$$F(a)=0.$$
由$\phi$为 Lipschitz 连续, 故存在一个常数$A$,满足
$$|F’(x)|=|\phi(x,f_1(x))-\phi(x,f_2(x))|\leqslant A|f_1(x)-f_2(x)|.$$
由以上引理, 显然$F\equiv 0$, 也就是说$f_1=f_2$.命题得证.
\end{proof}

现在,为了对常微分方程的解的增长”形态”有一个定性的了解. 考察以下微分不等式:
$$f’(x)\leqslant \gamma f(x)^\beta$$
其中$f$为一个正函数, $\gamma$为某一常数,而$0\leqslant\beta<1$.

设对于$x\geqslant a$, 函数$f$满足以上不等式. 令$g:=f^{1-\beta}$,则有
$$g’(x)=(1-\beta) f^{-\beta}(x)f’(x)\leqslant \gamma(1-\beta).$$
设$g(a)=c$, 那么结合前面的推论(\ref{cor:3}), 容易验证,对于$x\geqslant a$, 有
$$g(x)\leqslant\gamma(1-\beta)(x-a)+c.$$
那么对于函数$f$,就有$$f(x)\leqslant(\gamma(1-\beta)(x-a)+c)^\frac{1}{1-\beta}.$$
这里可以看到,$f$渐进增长的趋势类似于幂函数$x^{\frac{1}{1-\beta}}$.

具体的可以总结为以下几类:

• $$f’=\gamma f.$$这种情况,$f(x)$正比于函数$e^{\gamma x}$, 也就是说这个解函数成指数级增长(exponential growth);
• $$f’=\gamma f^{\alpha}\quad(\alpha>1).$$这种情况下, 正的解函数呈现爆炸式的增长,也就是说在某些有限的区间上,函数值可以向无穷大增长.有时也称其双曲增长(Hyperbolic growth).
• $$f’=\gamma f^{\beta}\quad(\beta<1).$$这种情况下, 解函数最多呈多项式增长(Polynominal growth).
• 当然,最简单的情况就是$f’=\gamma$.此时, 解函数呈线性增长(Linear growth).