Review - $\mathbb{R}^{n}$ 上的拓扑(2)

继续上一篇笔记, 接下来关注两个重要的拓扑性质——极限和连续.

连续

从拓扑结构出发刻画 连续

关于一般拓扑空间的连续性, 有多个等价定义和命题[1], 这里暂且只提最基本的一个.

从拓扑空间 $(X,\mathscr{T})$ 到拓扑空间 $(Y,\mathscr{U})$ 内的映射 $f$ 称为连续的, 当且仅当对于 $\mathscr{U}$ 中的每一个开集, 其在 $\mathscr{T}$ 中的原像为开集; 每一个闭集, 其在 $\mathscr{T}$ 中的原像为闭集.

换一种描述可能更有利于理解:

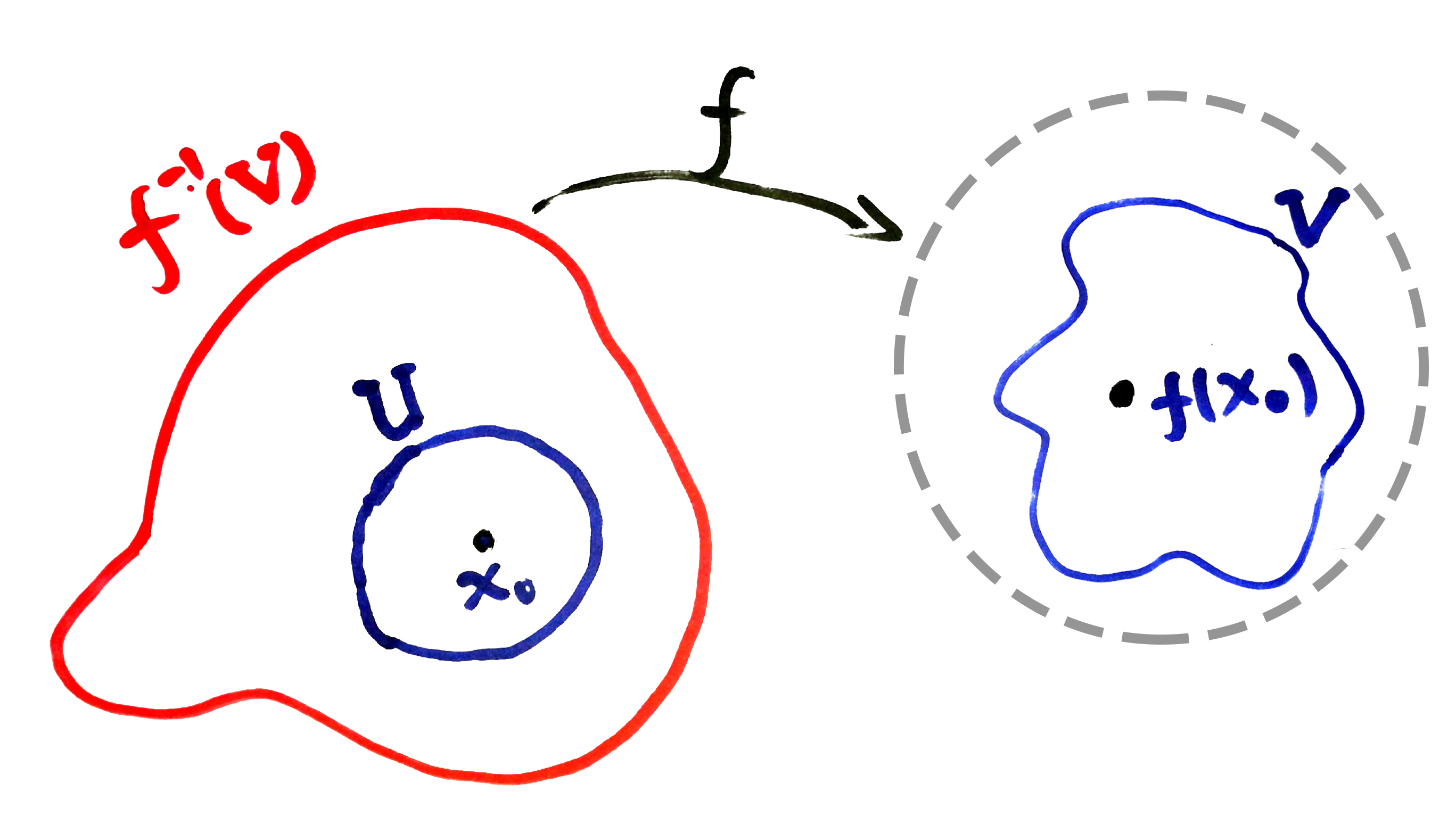
从拓扑空间 $(X,\mathscr{T})$ 到拓扑空间 $(Y,\mathscr{U})$ 内的映射 $f$ 称为在 $x_0$ 点连续, 如果映射满足: 任取 $f(x_0)$ 的邻域 $V$, 存在 $x_0$ 的邻域 $U$, 使得 $U \subset f^{-1}(V)$. 若 $f$ 在 $(X,\mathscr{T})$ 的每一点都是连续的, 则称 $f$ 是连续的.

连续映射

NOTE: 定义中所表达的含义, 简而言之, 即要求邻域的原像是邻域(如图所示). 这保证了只要点 $x$ “落在” $x_0$ 的邻域 $U$ 内, $f(x)$ 也就落在了 $V$ 内. 而如果我们这样要求:”邻域的像是邻域”, 那么可以存在这样的情况: 即 $V\subset f(U)$ (如图中灰色虚线), 同时 $U\subset f^{-1}(V)$ —— 而这意味着, 存在点落在 $x_0$ 的邻域 $f^{-1}(V)$ 内, 但其像落在 $f(x_0)$ 的邻域 $V$ 外, 显然这是不合理的

引入度量描述的连续

令 $X$ 和 $Y$ 是分别带有度量 $d_{X}$ 和 $d_{Y}$ 的度量空间.

映射 $f$ 在 $x_0$ 点连续, 当且仅当: $\forall~\varepsilon>0$, $\exists~\delta>0$, 使得当 $d_{X}(x,x_{0})<\delta$ 时, $$d_{Y}(f(x),f(x_{0}))<\varepsilon.$$

这正是很经典的 $\varepsilon-\delta$ 语言的连续性的表达.

【几个连续映射的例子】常值映射 $e_{b}: X\rightarrow Y, \quad x\mapsto b$; 恒等映射 $id_{X}:X\rightarrow Y, \quad x\mapsto x$.

有一种特别要指出的情况, 如果点 $x_{0} \in X$ 的 $\delta$ 邻域内只包含 $x_0$ 自己这一个点, 那么 $x_{0}$ 是 $X$ 上的孤立点. 按照以上连续性的定义, 显然, 任何一个映射 $f$ 在孤立点都是连续的. 另外, 在 $X$ 上一点 $x_0$ 上连续的映射 $f$, 在包含 $x_0$ 的 $X$ 的一个子空间 $A$ 上的限制 $f\mid_{A}:A\rightarrow Y$ 在$x_0$ 上依旧连续.

回到 $\mathbb{R}^{n}$ 上来, 我们有以下定理:

**定理**

$X$ 是一个度量空间, $f:X\rightarrow \mathbb{R}^{n}$ 具有形式: $f(x)=(f_{1}(x),f_{2}(x),\cdots,f_{n}(x))$, 则 $f(x)$连续当且仅当其每一分量函数 $f_{i}(x)$ 连续.

$f, g: X \rightarrow \mathbb{R}^{n}$ 在点 $x_0$ 连续, 则 $f+g$, $f-g$, $f\cdot g$ 都在点 $x_0$ 连续. $g(x_0)\neq 0$ 时, $f/g$ 也在点 $x_0$ 连续.

由 $\pi_{i}(\mathbf{x})=x_{i}$ 给出的投影函数是连续的.

极限

下面来定义极限这一概念.

设 $X$ 为一个度量空间, $x_0$ 为 $f$ 的定义域 $A\subset X$ 的极限点(不要求 $x_0 \in A$). 若对于 $Y$ 的任意一个包含 $y_0$ 的开集 $V$, 均有包含 $x_{0}$ 的开集 $U$, 使得对于 $x\in U \cap A, x\neq x_0$ 有 $f(x)\subset V$, 则称 $x$ 趋于 $x_0$ 时 $f(x)$ 趋于 $y_0$.

用包含度量的方法描述, 就是

当 $x$ 趋于 $x_0$ 时 $f(x)$ 趋于 $y_0$, iff $\forall~\varepsilon>0$, $\exists~\delta>0$, 使得当 $x \in A$ 且 $0< d_{X}(x,x_{0})<\delta$ 时, $$d_{Y}(f(x),y_{0})<\varepsilon.$$

这一极限的定义, 就是经典的极限的 $\varepsilon-\delta$ 定义. 极限的各项运算法则容易证明也是成立的.

这一篇笔记的最后用极限和连续性之间关系的一个很熟悉的定理结尾:

**定理**: 令 $f:X\rightarrow Y$. 若 $x_{0}$ 是 $X$ 上的孤立点, 则 $f$ 在 $x_0$ 连续; 否则, $f$ 在 $x_0$ 连续 iff $x$ 趋于 $x_0$ 时 $f(x)$ 趋于 $f(x_{0})$.

[1] J. L. 凯莱. 一般拓扑学. 科学出版社(北京), 2010. Page57.

[2] Note: 映射连续的定义中并未涉及到映射的类型. 若映射 $f$ 是一个双射(一一映射), 且 $f$ 与 $f^{-1}$ 均连续, 则称 $f$ 为同胚, 称 $X$ 和 $Y$ 同胚或拓扑等价. 这种映射是立即的一步到位的变化, 而谈到拓扑, 很多人往往想到的是一个连续变形的过程, 其实这种过程是拓扑中的另一个概念: 同伦.

NEXT: 内部和边界