Review - $\mathbb{R}^n$ 上的拓扑(1)
 这篇笔记主要内容是回顾 $\mathbb{R}^n$ 上的拓扑. 事实上,这里是要对由度量诱导的 $\mathbb{R}^n$ 的度量空间上的拓扑进行总结. 对于一般的拓扑空间(不依赖特定度量的性质)的拓扑性质, 更为详细的内容, 可以参考任意一本《点集拓扑学》或《一般拓扑学》之类的讲义. 事实上, 度量空间上的极限, 连续性, 和紧性都是空间拓扑性质的例子.
这篇笔记主要内容是回顾 $\mathbb{R}^n$ 上的拓扑. 事实上,这里是要对由度量诱导的 $\mathbb{R}^n$ 的度量空间上的拓扑进行总结. 对于一般的拓扑空间(不依赖特定度量的性质)的拓扑性质, 更为详细的内容, 可以参考任意一本《点集拓扑学》或《一般拓扑学》之类的讲义. 事实上, 度量空间上的极限, 连续性, 和紧性都是空间拓扑性质的例子.
度量空间
首先给出度量空间的定义.
给定一个集合 $X$, 定义其上的度量为一个映射 $d: X\times X \rightarrow \mathbb{R}$, $\forall x, y, z \in X$, 满足: - $d(x, y)=d(y, x)$. - $d(x, y)\geq 0$, 等号成立 iff $x=y$. - $d(x, z)\leq d(x,y) +d(y,z)$. 集合 $X$ 连同其上的度量 $d$ 一起构成了一个**度量空间**. 可以看到, 对于度量空间 $X$ 的子集 $Y$, 度量 $d$ 在 $Y\times Y$ 上的限制也是 $Y$ 的度量. 即 $Y$ 也构成一个度量空间.
[两种常用度量]
在 $\mathbb{R}^n$ 上常用的度量有两个:
$$d(\mathbf{x,y})=\Vert \mathbf{x-y} \Vert;$$
$$d(\mathbf{x,y})=\vert \mathbf{x-y} \vert.$$
这两者分别称为 Euclid 度量和确界度量.
$\mathbb{R}^{n}$ 上由 Euclid 度量诱导的拓扑, 形成的拓扑空间称为欧氏空间.
邻域, 开集, 闭集
设 $X$ 是带度量 $d$ 的度量空间. 给定 $x_{0}\in X$ 以及任意的 $\varepsilon >0$, 称集合
$$U(x_{0}, \varepsilon)=\{ x\mid d(x,x_{0})<{\varepsilon} \}$$
为 $x_{0}$ 的 $\varepsilon$ 邻域.
若对于 $X$ 的子集 $U$, $\forall x_{0}\in U$, $\exists \varepsilon>0$, 使得 $U(x_{0},\varepsilon)\subset U$, 那么, 称 $U$ 为 $X$ 上的开集, 其余集 $X-U$ 则称为闭集. 若 $U$ 是包含 $x_{0}$ 的任意开集, 则直接称 $U$ 为 $x_{0}$ 的邻域.
在 $\mathbb{R}^{n}$ 中, 按照 Euclid 度量, 对于 $\mathbf{a}\in \mathbb{R}^{n}$的 $\varepsilon$ 邻域, 称为以 $\mathbf{a}$ 为中心, $\varepsilon$ 为半径的开球, 记为 $B(\mathbf{a},\varepsilon)$; 按照确界度量, 则称为以 $\mathbf{a}$ 为中心 $\varepsilon$ 为半径的开立方体, 记为 $C(\mathbf{a},\varepsilon)$.
关于度量空间上的开集和闭集, 有几个常见的性质:
**定理 1** $(X,d)$ 为一个度量空间, 则 $X$ 中的开集的**有限交**与**任意并**, 都是 $X$ 中的开集. Likewise, $X$ 中的开闭集的**任意交**与**有限并**, 都是 $X$ 中的闭集.
注: 开集的任意交不一定是开集, 闭集的任意并也不一定是闭集, 例如:
$$\bigcap_{n=1}^{\infty}{\left( -\frac{1}{n}, \frac{n+1}{n} \right)}=[0,1];$$
$$\quad \bigcup_{n=1}^{\infty}{\left[ \frac{1}{n}, 1-\frac{1}{n} \right]}=(0,1).$$
我们在一个度量空间 $X$ 上定义了开集, 同样的可以在其子空间 $Y$ 上同样的定义开集. 这两者之间有如下这样的简单的关系.
定理 2 $X$ 是一个度量空间, 而 $Y$ 是 $X$ 的一个子空间.则 $Y$ 的一个子集 $A$ 是开集, 当 $A=U\cap Y$, 其中 $U$ 是 $X$ 中的开集; $A$ 是闭集, 当 $A=C\cap Y$, 其中 $C$ 是 $X$ 中的闭集.
值得注意的一点, 集合的包含关系上看, $A\subset Y\subset X$, 但是 $A$ 作为 $Y$ 上的开集, 可以不是 $X$ 上的开集; 同样 $A$ 可以是 $Y$ 上的闭集, 但不是 $X$ 上的闭集.
【两个例子】 1) 在定义了欧氏度量的 $\mathbb{R}^{2}$ 空间上, 任取一点 $O$ 为原点, 建立直角坐标系. 其子空间 $\mathbb{R}$ 上的开区间 $(a,b)$. 显然$(a,b)$ 是 $\mathbb{R}$ 上的开集, 但不是 $\mathbb{R}^{2}$ 上的开集.
2) 同样在定义了欧氏度量的 $\mathbb{R}^{2}$ 空间上, 在去掉原点后的部分, 即 $\mathbb{R}^{2}\O$ 是 $\mathbb{R}^{2}$ 的一个子空间, 以 $x$ 轴为分界线, 取包括x轴在内的下半平面, 记为 $S$, 显然 $S$ 是 $\mathbb{R}^{2}\O$ 上的闭集, 但不是 $\mathbb{R}^{2}$ 上的闭集.
聚点(极限点)与闭包
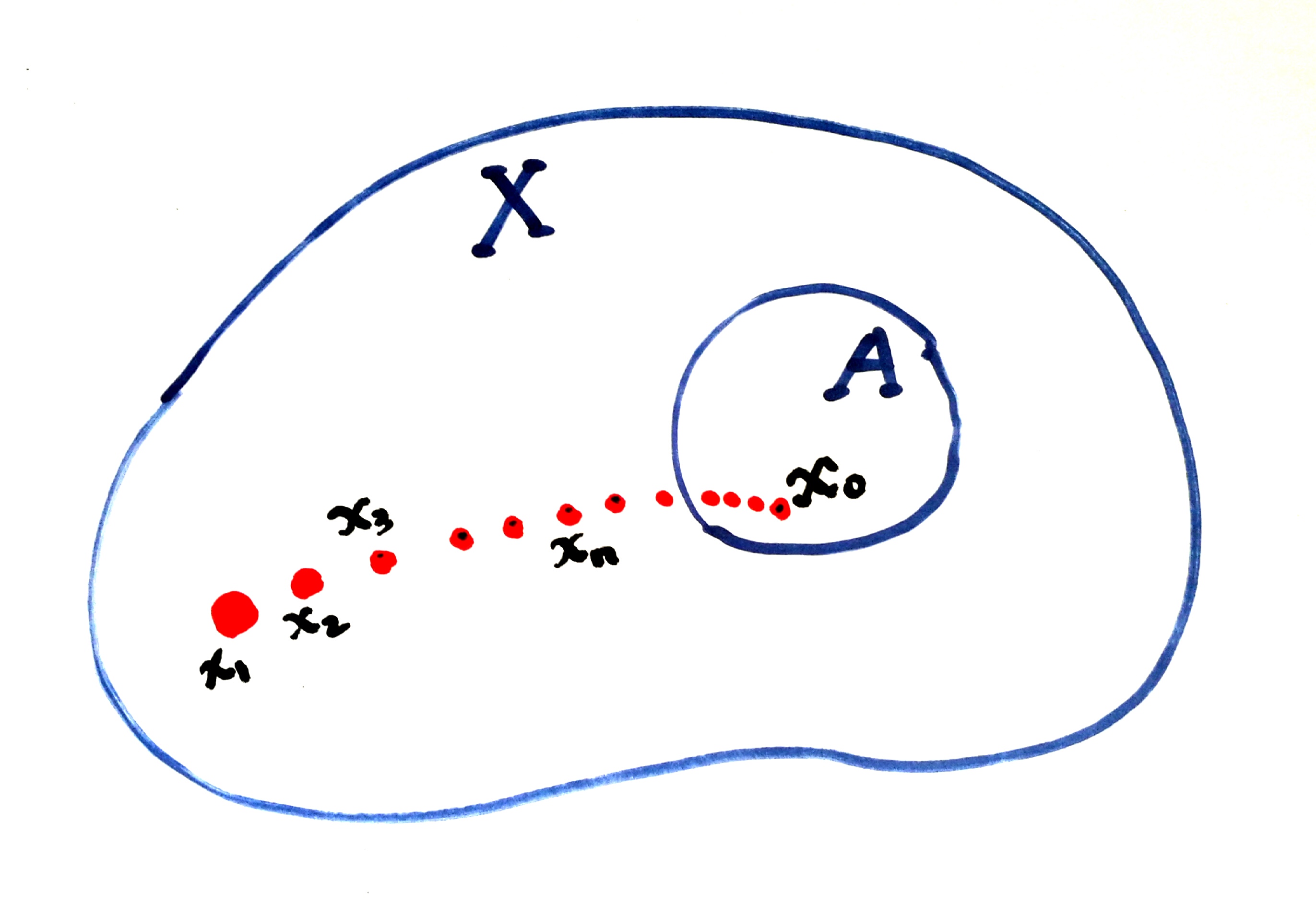
设 $X$ 为一个度量空间, 对于 $x_{0}\in X, A\subset X$, 若 $\forall \varepsilon>0$, $U(x_{0},\varepsilon)\cap A\neq \varnothing$, 则称 $x_0$ 为 $A$ 的极限点(聚点).
定理 3 设 $A$ 是 $X$ 的子集, 那么包含 $A$ 以及其所有极限点的集合 $\overline{A}$ 是 $X$ 上的闭集.
$\overline{A}$ 称为 $A$ 的闭包, 而所有极限点构成的集合 $A’$ 称为 $A$ 的导集.
由此我们得到判断闭集的一个充分必要条件:
$X$ 的一个子集是闭的当且仅当 $A=\overline{A}$.
内部和边界
内部和边界的概念, 对于任意的拓扑空间都是有意义的, 可以直接应用到 $\mathbb{R}^{n}$ 上. 并且这一概念与闭包有着密切的联系.
我们称拓扑空间的子集 $A$ 的点 $x$ 为 $A$ 的内点, 如果 $A$ 是 $x$ 的邻域. 集合 $A$ 的所有内点组成的集合称为 $A$ 的内部, 记作 $A^{0}$ 或 $\text{Int} A$.
定理 4 设 $A$ 为拓扑空间 $X$ 的子集, 则 $A$ 的内部 $A^{0}$ 是开集, 且是 $A$ 的最大开子集; $A$ 为开集 iff $A=A^{0}$; $A$ 中所有不是 $X\sim A$ 的聚点的点所构成的集合恰是 $A^{0}$; $X\sim A$ 的闭包是 $X\sim A^{0}$.
拓扑空间的子集 $A$ 的边界, 指所有既不属于 $A$ 也不属于 $X\sim A$ 的点构成的集合. 记为 $\text{Bd}A$.
显然, 对于在 $x\in \text{Bd}A$, 对于所有包含 $x$ 的开集, 同时与 $A$ 和 其余集 $X\sim A$ 相交.
Next Part: 极限与连续性
Review - $\mathbb{R}^n$ 上的拓扑(1)

