切空间与切丛

本文旨在以简单直观的方式介绍切空间与切丛的概念, 为之后的一系列准备发布的内容做知识上的准备.

在此, 有必要先辨析两个概念:”向量空间”, “流形”.

“向量空间”, “流形”之概念

向量空间, 顾名思义, 以向量为元素构成的线性空间. 通常用列向量
$$\overrightarrow{v} = \begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{pmatrix}$$
来表示 $n$ 维向量空间中的元素 $\overrightarrow{v}$.

而流形, 是满足特定性质一个点集, 不严格的, 我们可以简单的说: “流形是局部欧几里得化的(或者说正则的)空间“, 直观来看, 当我我们放大观察一个 $n$ 维流形的局部区域, 这个局部足够”平坦”, 以至于近似的可以视为欧几里得空间 $\mathbb{R}^n$. 显然, 其元素是一个个点
$$x:=(x_1, x_2, \cdots x_n).$$

这两个概念有时容易混淆, 比如 $\mathbb{R}^n$, 这是 $n$ 维欧氏空间的符号, 可以代表 $n$ 维向量空间, 本身也是一个 $n$ 维流形. 具体写法上, 给定坐标系后都可以写出 $n$ 个分量, 但是, 必须明确, 我们谈到”向量空间 $\mathbb{R}^n$ “时, 每个元素是由给定的坐标原点出发到终点为相应坐标的向量, 而谈到”流形 $\mathbb{R}^n$ “时, 其每个元素是点.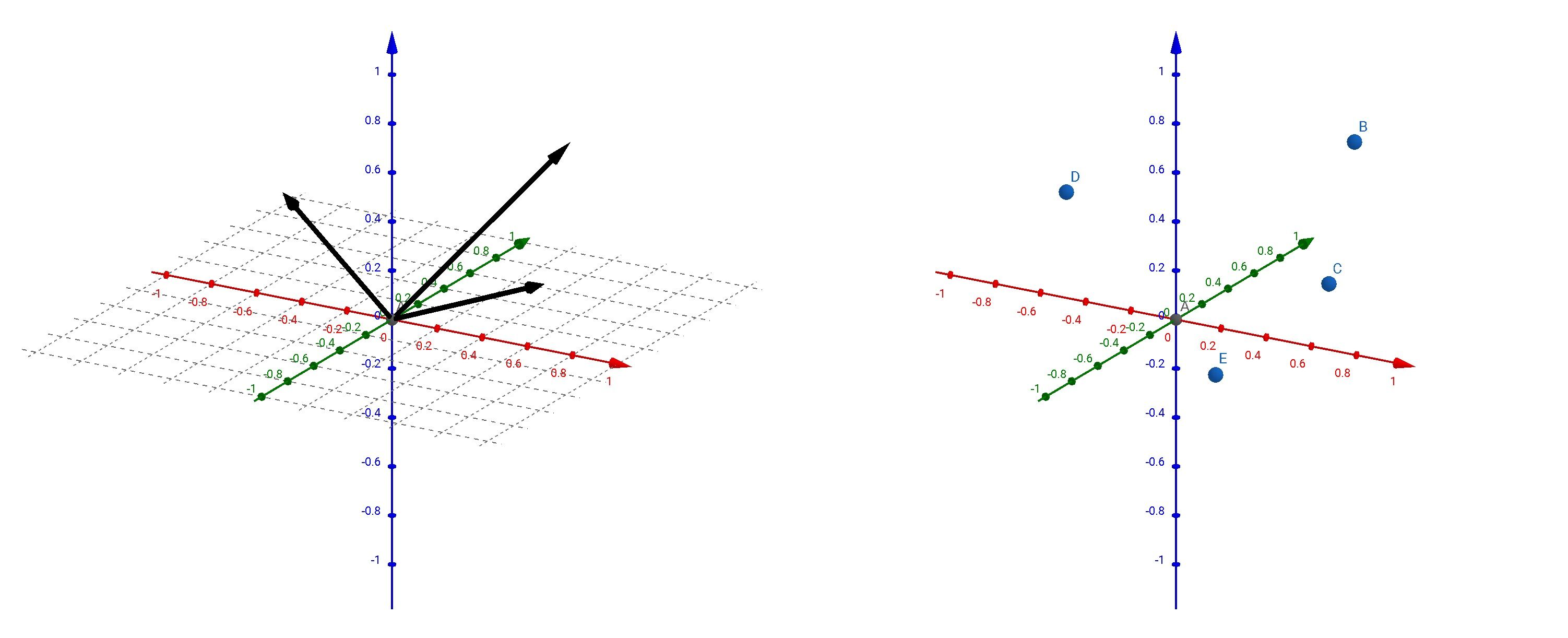

搞清楚我们是在哪里做运算, 这是在理解问题上是很重要的.

切空间 (Tangent Space)

先直观的感受一下.

• 平面上的给出一条光滑曲线, 对于其上的给定的一个点 $p$ 可以给出相应的曲线的切线. 由点 $p$ 出发终点位于这条切线上的向量, 自然称为曲线在这一点处的切向量.
  显然, 曲线在点 $p$ 处的全部切向量构成一个向量空间 $\mathbb{R}$.

• 球面 $S^2$ 是一个 2 维流形, 对于其上的给定的一个点可以给出相应的切平面, 由该点出发终点位于这个切平面上的向量, 也可以称为切向量. 显然, 球面在该点处的全部切向量构成一个向量空间 $\mathbb{R}^2$, 每个切向量也对应着球面上一个大圆, 是相应的大圆在这一点处的切向量.

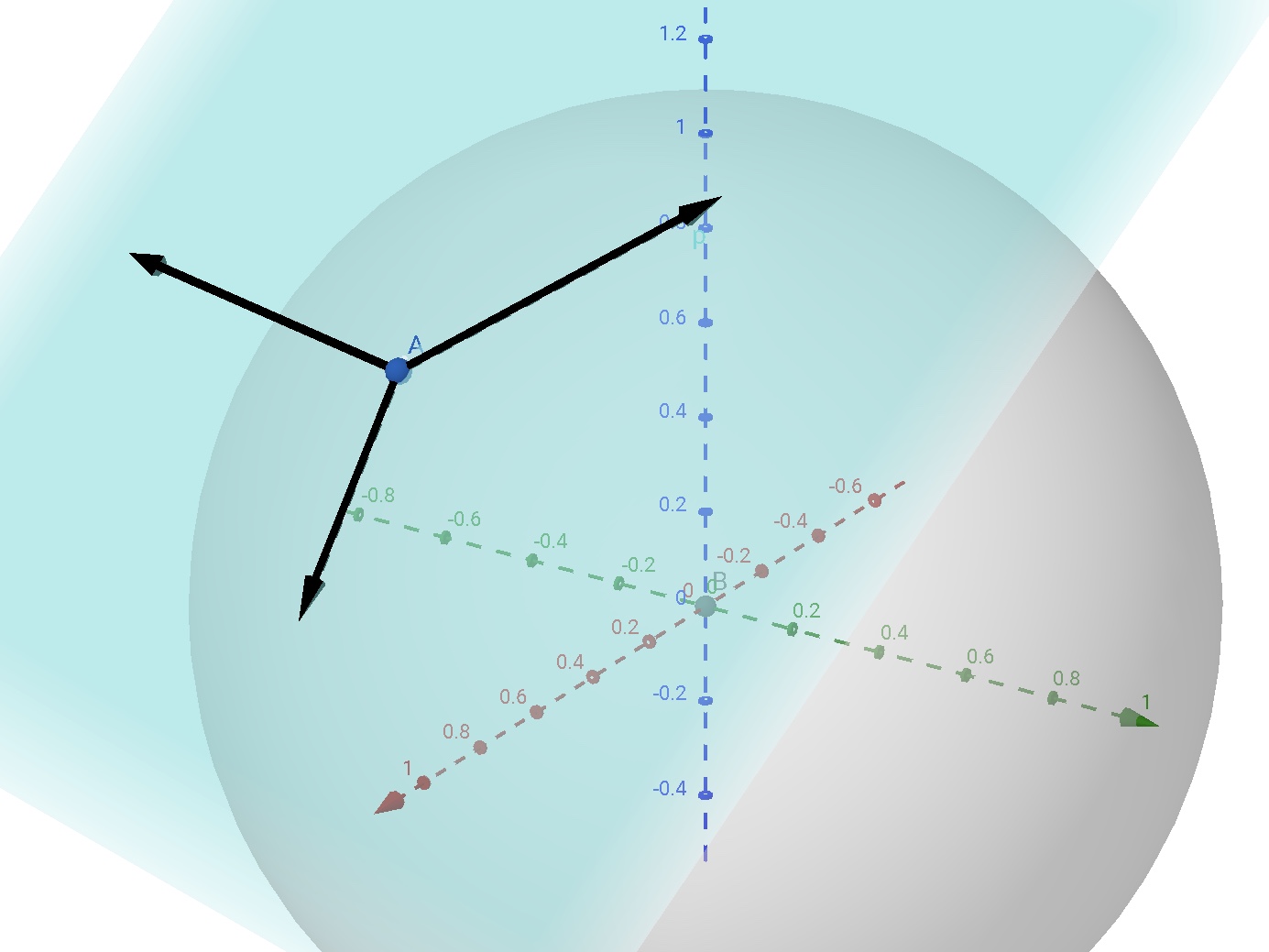
其实以上切向量构成的向量空间, 均为切空间的例子. 下面给出严格的定义:

【定义】光滑流形 $M$ 在一点 $p$ 处的切空间, 是由 $M$ 上所有通过点 $p$ 的曲线在 $p$ 处的切向量所构成的空间. 用符号 $TM_{p}$ 或 $T_p M$ 表示.

注意到, 在光滑流形的每一点处都有相应的切空间.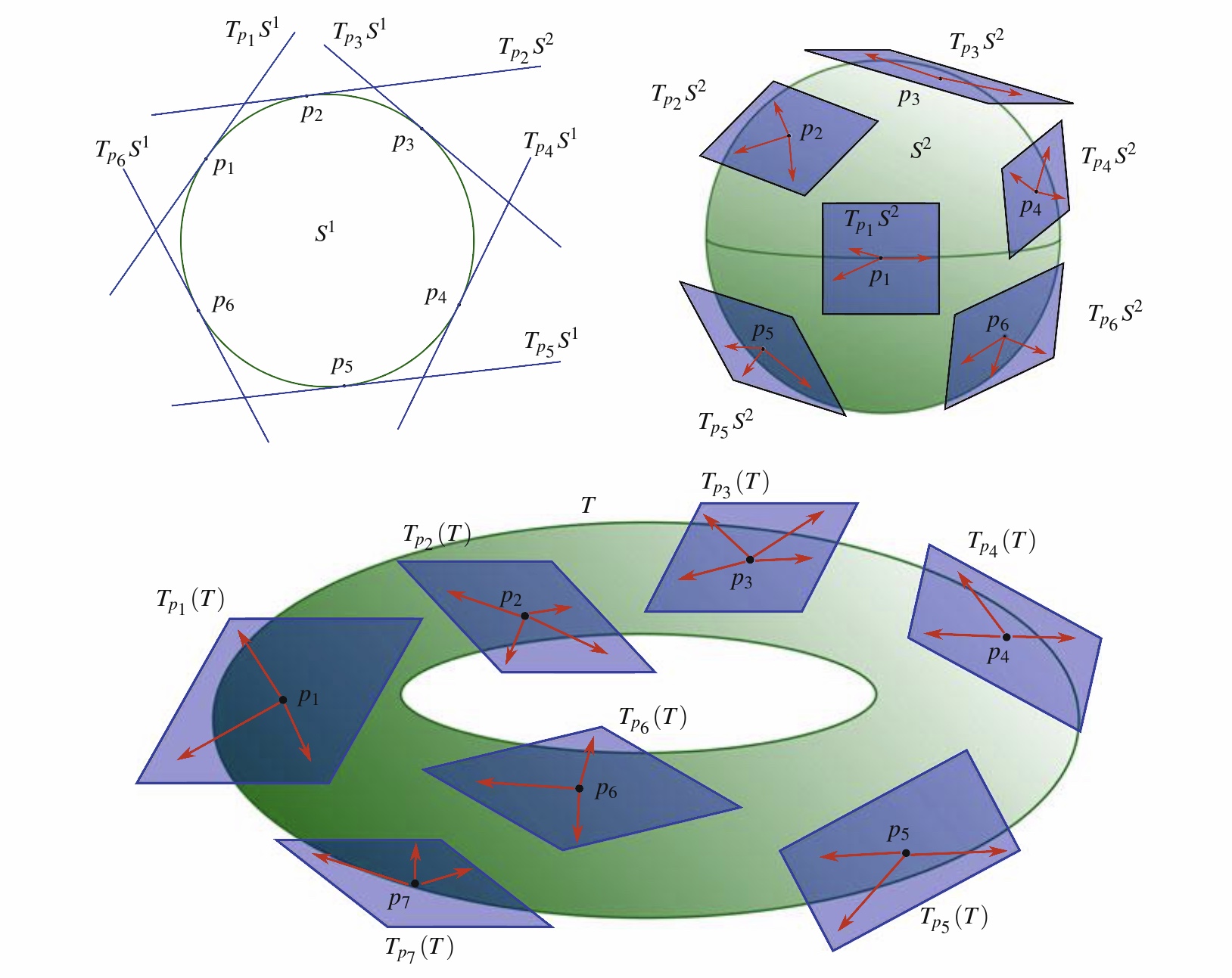

切丛 (tangent bundle)

直观的说, 对于流形 $M$, 沿着其上每一点构成的切空间, 称之为流形 $M$ 的切丛, 一般用符号 $TM$ 表示. 事实上, 流形 $M$ 的切丛也构成一个流形.

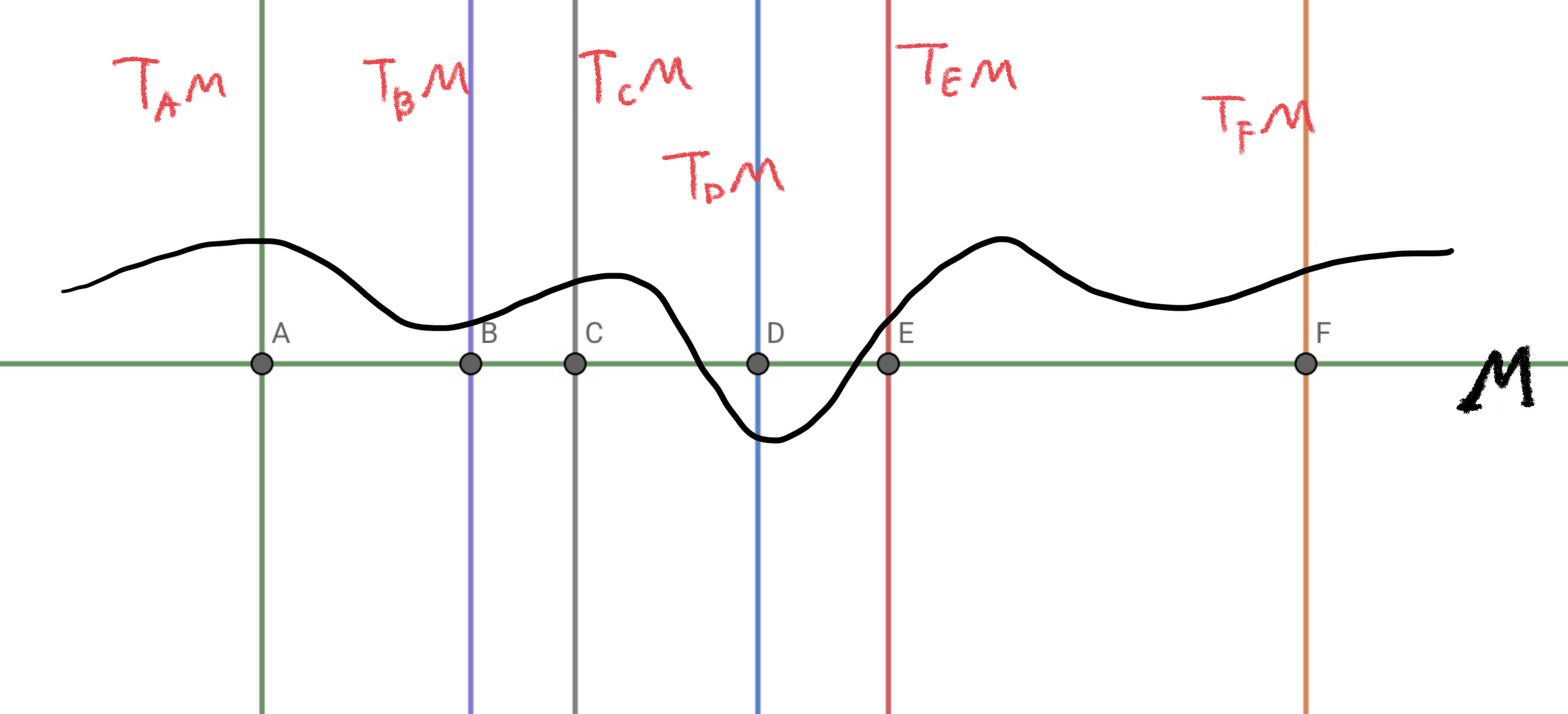
可以这样去想象, 用水平坐标轴表示流形 $M$, 其上每一点处的切空间用过这一点的垂线表示, 而所得到的这个平面便可以表示切丛 $TM$.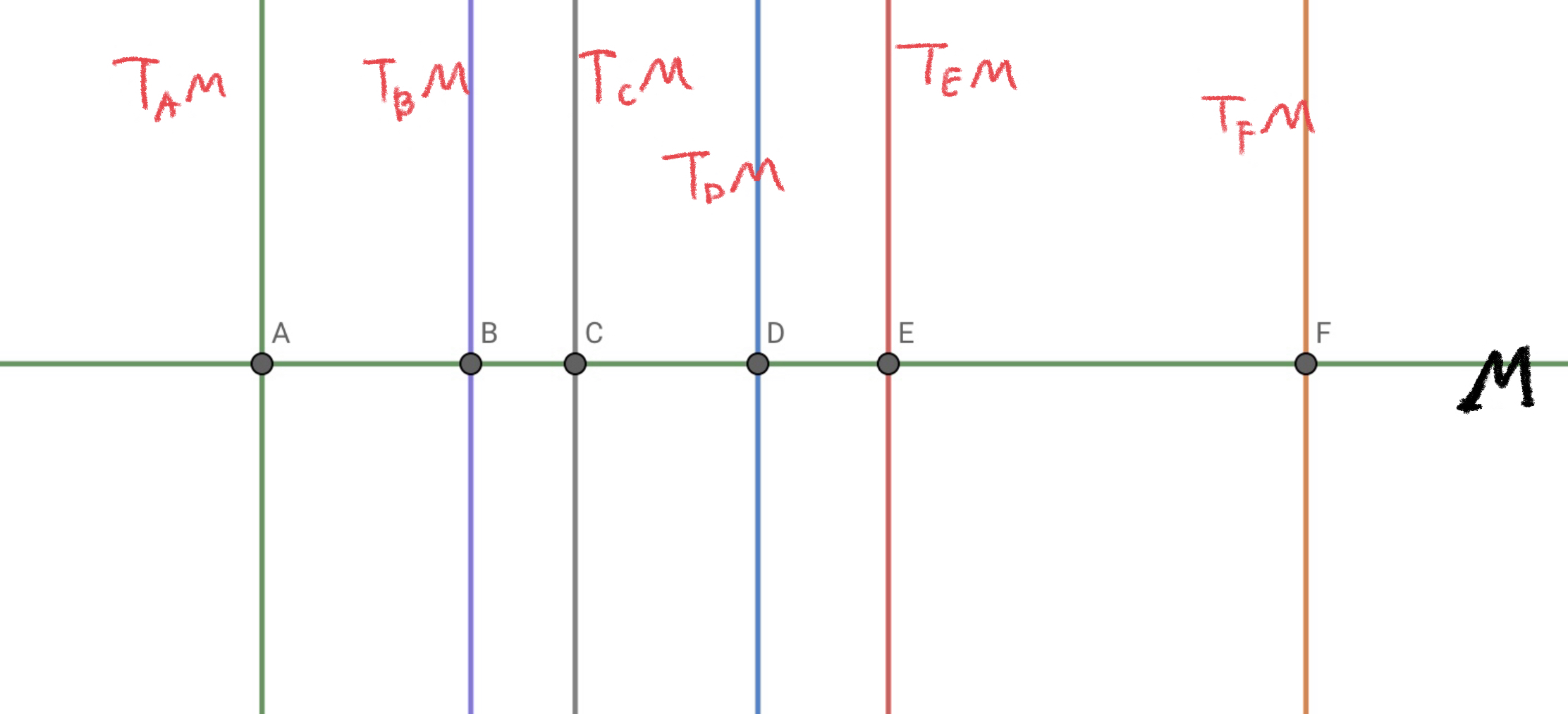

关于切丛, 容易看到以下性质:

$n$ 维流形 $M$ 的切丛 $TM$ 是 $2n$ 维的.

可以这样理解这件事: 为了给出切丛上的一个”点”, 首先需要 $n$ 个坐标描述 $M$ 上的一个点 $p$, 然后需要 $n$ 个由 $p$ 出发的基向量来描述这一点处的切空间, 合起来, 也就是需要 $2n$ 个”分量”.

另外, 我们可以在流形上给定向量场 (Vector Field), 即在每个点处给定一个向量. 学过微分方程应该知道, 连续的向量场给出一系列曲线, 向量场中的每个向量都是这些曲线中某一条的切向量. 这些曲线称之为积分曲线.

同时注意到, 向量场中每个向量都属于某个切空间, 所以整个向量场相当于在切从上”切了一刀”, 称之为切丛截面.