洛伦兹变换的数学推导

作为数学的一个简单的在物理上应用的例子, 这里我们写一写爱因斯坦狭义相对论中的洛伦兹变换的推导. 关于狭义相对论的具体物理理论、背景和发展, 参考 Wiki-狭义相对论.

狭义相对论两条基本假设

狭义相对论由爱因斯坦在1905年完成的《论动体的电动力学》论文中提出. 其基础有两条假设:

• 光速不变
• 狭义相对性原理

光速不变 说的是在所有惯性系中，真空中的光速都等于 $c= \frac {1}{\sqrt {\mu _{0}\epsilon _{0}}}$ 与光源运动无关(这一点来自于麦克斯韦方程); 而狭义相对性原理, 则说明在所有惯性系中，物理定律有相同的表达形式。这是力学相对性原理的推广，它适用于一切物理定律，其本质是所有惯性系平权。

我们将从这两个基本假设开始, 推导出洛伦兹变换, 而所谓尺缩效应和钟慢效应都是随之而来的自然结果. 为此先回顾一些数学的基本知识.

一点数学知识

双曲函数

类似于圆函数 $\sin x$ 和 $\cos x$, 有一类函数称为双曲函数, 其解析定义如下:
$$\sinh x = \frac{e^x - e^{-x}}{2},\quad \cosh x = \frac{e^x + e^{-x}}{2} $$
分别称为 双曲正弦 和 双曲余弦.
类似正切函数, 定义 $\tanh x = \frac{\sinh x}{\cosh x}$ 为双曲正切.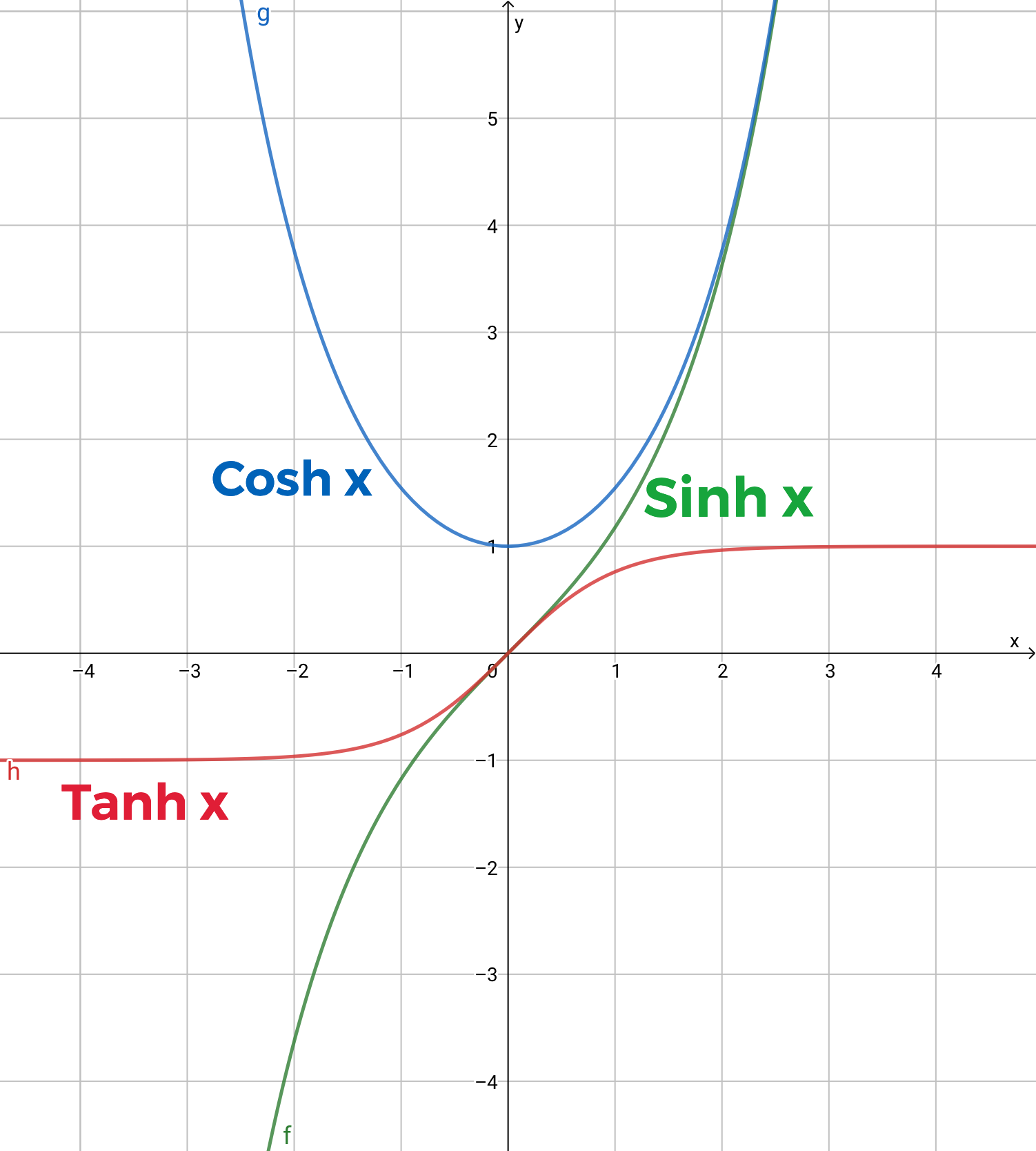

容易从定义验证, 双曲函数具有类似于圆函数以下性质:

• $\cosh^2 x - \sinh^2 x = 1$;
• $\sinh’ x = \cosh’ x$;
• $\cosh’ x = \sinh x$.

隐函数的微分法

设函数 $x = x(t)$, $y = y(t)$ 均为在 $t_0\in \mathbb{R}$ 的邻域 $U(t_0)$ 有定义的函数. 并且函数 $x = x(t)$ 有反函数 $t = t(x)$. 于是函数 $y$ 可视为关于 $x$ 的隐函数.

在 $x(t_0)\neq 0$ 的情况下, 隐函数的导数(即 $y$ 关于 $x$ 的导数)为(应用复合函数与反函数求导法则):
$$\frac{dy}{dx} = \frac{dy(t(x))}{dx} = \frac{dy}{dt}\frac{dt}{dx}=\frac{dy}{dt}/\frac{dx}{dt}.$$

线性变换

设 $X$ 为一个线性空间, 则线性映射 $\tau := X\rightarrow X$ 称为 $X$ 上的一个线性变换.

线性变换可以表示为矩阵形式, 以 $\mathbb{R^2}$ 上的线性变换为例, 设 $(x,t)$ 为 $\mathbb{R^2}$ 上对应某一坐标系的一点, 经过以下线性变换后 (\ref{eq:xxbh}), 在新的坐标系下坐标为 $(\widetilde{x},\widetilde{t})$.
\begin{equation}
\label{eq:xxbh}
\begin{cases}
\widetilde{x} = \alpha x + \beta t \\
\widetilde{t} = \gamma x + \delta t
\end{cases}
\end{equation}
用矩阵形式表示, 就是
\begin{equation}
\label{eq:xxbhjz}
\begin{pmatrix}
\widetilde{x}\\
\widetilde{t}
\end{pmatrix} = \begin{pmatrix}
\alpha & \beta \\
\gamma & \delta
\end{pmatrix}\begin{pmatrix}
x \\
t
\end{pmatrix}.
\end{equation}
当对于变换矩阵 $\det\begin{pmatrix}
\alpha & \beta \\
\gamma & \delta
\end{pmatrix}\neq 0$ 时, 称这个变换为非退化的. 也就是说矩阵可逆, 或者说线性变换时可逆的, 即 $(x,t)$ 也可以表示为 $(\widetilde{x},\widetilde{t})$ 的线性变换.

线性变换下的速度公式

我们用 $\overrightarrow{x}$ 表示一个质点的在给定坐标系中的位移, $t$ 表示该坐标系的时间; $\widetilde{x}$ 与 $\widetilde{t}$ 表示在变换后的坐标系中的位移和时间. 现在我们可以给出在给定坐标系 中以速度 $\overrightarrow{v}$ 运动的点的速度, 在给定的线性变换 (\ref{eq:xxbhjz}) 下的公式了. 用 $\widetilde{v}$ 表示在新坐标系下的速度.

首先, 我们知道速度是位移的导数, 即
$$\overrightarrow{v} = \frac{d\overrightarrow{x}}{dt},\quad \widetilde{v} = \frac{d\widetilde{x}}{d\widetilde{t}}.$$

由隐函数的求导法则, 可以得到关于速度的变换公式:
\begin{equation}
\widetilde{v} = \frac{d\widetilde{x}}{dt}/\frac{d\widetilde{t}}{dt} = \frac{\alpha\frac{d\overrightarrow{x}}{dt} + \beta}{\gamma\frac{d\overrightarrow{x}}{dt} + \delta} = \frac{\alpha\overrightarrow{v} + \beta}{\gamma\overrightarrow{v} + \delta}.
\end{equation}

洛伦兹变换的导出

现在来导出洛伦兹变换.

根据光速不变的假设, 在不同坐标系下, 测得的光速是一致的. 设在初始时刻, 质点在两个坐标系中位移均为 $0$, 即 $t = \widetilde{t} = 0$ 时, $\overrightarrow{x} = \widetilde{x} = 0$. 从 $(\overrightarrow{0},0)$ 处发出一束光, 显然, 在这两个坐标系下我们有
$$\overrightarrow{x}^2-c^2 t^2 = \widetilde{x}^2-c^2 \widetilde{t}^2.$$
(这里取平方, 是为了将矢量运算变为数量的运算, 也便于导出下面的方程组.)

由线性变换关系 (\ref{eq:xxbh}), 由上式我们得到以下方程组:
\begin{cases}
\alpha^2 - c^2\gamma^2 = 1\\
\alpha\beta-c^2\gamma\delta = 0\\
\beta^2 - c^2\delta^2 = -c^2
\end{cases}

考虑双曲函数的性质, 容易给出方程组的通解为:
\begin{equation}
\label{eq:llz1}
\begin{pmatrix}
\alpha & \beta\\
\gamma & \delta
\end{pmatrix}=\begin{pmatrix}
\cosh\theta & c\sinh\theta\\
\frac{1}{c}\sinh\theta & \cosh\theta
\end{pmatrix}
\end{equation}
其中 $\theta$ 为某个由变换确定的参数.

上式 (\ref{eq:llz1}) 中给出的就是著名的洛伦兹变换.

我们假设新坐标系相对于原坐标系以速度 $\overrightarrow{v_0}$ 运动. 即 $\widetilde{x} = \overrightarrow{0}$ 这一点在原坐标系中的速度为 $v_0$, 由 (\ref{eq:llz1}) 有 $0 = \overrightarrow{x}\cosh \theta + c t\sinh \theta$, 即
$$\tanh \theta = -\frac{\overrightarrow{v_0}}{c}.$$

由双曲函数性质, 容易得到
$$\cosh \theta = \frac{1}{\sqrt{1-\tanh^2 \theta}} = \frac{1}{\sqrt{1-\frac{v_0^2}{c}}}.$$

物理上称上式中 $\frac{1}{\sqrt{1-\frac{v_0^2}{c}}}$ 为洛伦兹因子.

于是我们可将洛伦兹变换化为
\begin{equation}\label{eq:llz2}
\begin{pmatrix}
\widetilde{x}\\
\widetilde{t}
\end{pmatrix} = \begin{pmatrix}
\frac{\overrightarrow{x} -\overrightarrow{v_0} t}{\sqrt{1-\frac{v_0^2}{c}}}\\
\frac{t-\frac{v_0^2}{c}x}{\sqrt{1-\frac{v_0^2}{c}}}
\end{pmatrix}
\end{equation}

这就是我们常见的洛伦兹变换的公式. 以上公式中, 当低速状态下 $v_0<< c$ 时, 便可近似成为
\begin{equation}
\begin{pmatrix}
\widetilde{x}\\
\widetilde{t}
\end{pmatrix} = \begin{pmatrix}
\overrightarrow{x} -\overrightarrow{v_0} t\\
t
\end{pmatrix},
\end{equation}
这便是我们熟知的伽利略变换.

同时, 从 (\ref{eq:llz2}) 可以看出, 相对于某物体运动的观察者所测量的在运动的那个轴向的长度，会比相对于物体静止的观察者测量到的同一长度要短(尺缩); 当质点运动时，它的一切（物理、化学变化）从其所在的参照系(坐标系)来看都会变慢(钟慢).

由洛伦兹变换出发, 狭义相对论的其他结果相应可以导出.