数学分析习题解-连续函数(1)
【习题来源】数学分析:第七版.(俄罗斯)卓里奇著;李植译. 北京:高等教育出版社,2019.
- 请证明:
a) 如果 $f\in C(A)$ 且 $B \subset A$, 则 $f|_ B = C(B)$.
b) 如果函数 $f: E_{1} \cup E_2 \rightarrow \mathbb{R}$, 满足 $f|_ {E_i} \in C(E_i), i = 1,2$, 则未必 $f\in C(E_1\cup E_2)$.
c) 黎曼函数 $\mathscr{R}$ 以及它在有理数集上的限制 $\mathscr{R}|_ {\mathbb{Q}}$ 在集合 $\mathbb{Q}$ 的每一个非零的点间断, 并且所有的间断点都是可去间断点.
【证明】
a) 由连续的定义直接得到.
b) 符号函数 $\text{sgn}(x)$ 就是一个例子. 在 $E_1 = (-\infty,0]$ 上函数为常值 $-1$, 在 $E_2 = (0,\infty)$ 上函数为常值 $1$, 都是连续的. 但在 $\mathbb{R}$ 上函数在 $x = 0$ 处间断.
c) 黎曼函数在无理点连续, 在有理点间断, 同时, 其任意一个点处的极限均等于 $0$, 显然, 常值函数 $f(x) = 0$ 连续, 且 $f| _{\mathbb{R\backslash Q}\cup 0} = \mathscr{R}| _{\mathbb{R\backslash Q}\cup 0}$. 有可去间断点定义, 结论是显然的. Q.E.D.
- 如果函数 $f\in C[a,b]$, 则函数 $m(x) = \min_{a\leq t\leq x}f(t)$, $M(x) = \max_{a\leq t\leq x}f(t)$ 也在闭区间 $[a, b]$ 连续.
【证明】 任取 $x_0\in [a,b]$, 由函数 $f$ 连续 $\forall \varepsilon >0, \exists \delta>0, \forall |x-x_0|<\delta$, 有 $|f(x)-f(x_0)|<\varepsilon$. 考察 $|m(x)-m(x_0)|$, 由其定义, 函数在 $[a,x_0]$ 上的最小值, 要么落在 $[a,x_0-\delta]$ 上, 要么落在 $x_0$ 的 $\delta$-邻域上. 对于前者有 $|m(x)-m(x_0)|= 0$, 对于后者有 $|m(x)-m(x_0)|< \varepsilon$. 于是 $m(x)$ 在 $x_0$ 处连续, 在 $[a,b]$ 上连续. $M(x)$ 同理可证. Q.E.D.
- 请证明:
a) 开区间上的单调函数的反函数在自己的定义域上连续.
b) 请构造一个具有可数个间断点的集合的单调函数.
c) 如果函数 $f:X\rightarrow Y$ 和 $f^{-1}:Y\rightarrow X$ 互为反函数($X,Y\subset \mathbb{R}$), 并且 $f$ 在点 $x_0\in X 连续$, 则由此还不能推出函数 $f^{-1}$ 在点 $y_0 = f(x_0)\in Y$ 连续.
【证明】
a) 先证明在区间上连续的单调函数的反函数在其定义域连续. ![一个例子: 函数 f(x) = x + [x]](https://i.loli.net/2019/08/04/GcE8nvC1PaeXoI4.png)
由于反函数存在的充分必要条件是函数在定义域上严格单调, 不妨设函数 $f: X\rightarrow Y$ 在区间 $X$ 上严格单调递增, 则其反函数也是严格单调递增的. 任取 $y_0 \in f(x_0), x_0\in X$. $\forall \varepsilon>0$, 可以取 $x_1<x_0<x_2\in U_X^{\varepsilon}(x_0)$, 由函数的严格单调递增, 有 $y_1 = f(x_1)<y_0<f(x_2) = y_2$. 取 $\delta = \min\{y_0-y_1,y_2-y_0\}$, 则当 $y\in U_Y^{\delta}(y_0)$ 时, 有 $y\in(y_1,y_2)$, 由反函数的单调性, 得到 $f^{-1}(y) = x \in U_X^{\varepsilon}(x_0)$. 由 $y_0$ 的任意性, 这便说明了 $f^{-1}$ 在区间 $X$ 内部(这是个开区间)上连续. 在 $X$ 的边界点上可以类似考虑.
再证明原命题. 考虑到单调函数只能有至多可数个第一类间断点. 故以这些间断点做划分, 可将原函数定义域划分为可数个开区间, 在这些开区间上, 函数是严格单调连续的. 而值域对应为可数个开区间(或半开半闭区间)的并. 由前面所证, 便得到原命题.
b) 取整函数就是一个典型例子. 还有右图所示 $f(x) = x+[x]$, 是另一个例子.
c) 令 $g^{-1}(x) = f(x)= x+[ x]$, $g(x) = f^{-1}(x)$, 这两个函数显然互为反函数, 但是, 在比如 $x=1$ 处, $g(x)$ 连续, 但是 $g^{-1}(x)$ 不连续. Q.E.D.
- 请证明:
a) 如果 $f,g\in C[a,b]$, 并且 $f(a)< g(a), f(b)> g(b)$, 则存在点 $c\in[a,b]$, 使得 $g(c)= f(c)$.
b) 闭区间 $[0,1]$ 到自身的任何连续映射 $f:[0,1]\rightarrow[0,1]$ 都有不动点, 即满足 $f(x) = x$ 的点 $x\in[0,1]$ 存在.
c) 如果闭区间到自身的两个连续映射 $f$ 和 $g$ 可交换, 即 $f\circ g =g\circ f$, 则他们的未必有共同的不动点. 然而, 例如线性映射和更一般的多项式总有不动点.
d) 连续映射 $f:\mathbb{R}\rightarrow\mathbb{R}$ 可以没有不动点.
e) 连续映射 $f:(0,1)\rightarrow(0,1)$ 可以没有不动点.
f) 如果映射 $f:[0,1]\rightarrow[0,1]$ 连续, $f(0)=0, f(1) = 1$, 并且在 $[0,1]$ 上 $(f\circ f)(x)\equiv x$, 则 $f(x)\equiv x$.
【证明】
a) 设函数 $F(x) = f(x) - g(x)$. 函数 $F$ 在 $[a,b]$ 上连续. 由波尔查诺-柯西中值定理(介值定理), 即得到结论.
b) 设函数 $F(x) = f(x) - x$. 函数 $F$ 在 $[0,1]$ 上连续, 并且 $F(0) = f(0)\in [0,1]$, $F(1) = f(1)-1\leq 0$. 显然, 要么 $x = 1$ 为一个不动点, 要么由介值定理即得到不动点的存在性.
c) 关于可交换连续映射的公共不动点是一个很有意思的课题. 这里给出一个篇参考文献COMMUTING FUNCTIONS WITH NO COMMON FIXED POINT, 其中给出了关于这一课题研究的情况, 以及一个没有公共不动点的例子.
d) 连续映射 $f(x) = x+1, (x\in \mathbb{R})$ 就是一个这样的例子.
e) 连续映射 $f(x) = \sin(\frac{\pi}{2}x), (x\in(0,1) )$ 就是一个这样的例子.
f) 首先, 映射 $f$ 是一个单射, (否则$\exists x_1\neq x_2\in [0,1]$, 使得$f(x_1) = f(x_2)$, 于是 $f\circ f(x_1) = f\circ f(x_2)$ 推出 $x_1 = x_2$.) 故 $f$ 在 $[0,1]$ 上严格单调. 于是必存在反函数 $f^{-1}: [0,1]\rightarrow[0,1]$. 于是 $\forall x \in[0,1]$, $f(x) = f^{-1}(x)$. 显然 $f(x)\equiv x$. Q.E.D
- 请证明: 闭区间上任何一个连续函数的值集也是闭区间.
【证明】 闭区间上的连续函数必能取到最大值与最小值. 设定义在闭区间 $X$ 上的函数 $f: X\rightarrow Y$, $Y\ni m = \min_{x\in X} f(x)$, $Y\ni M= \max_{x\in X} f(x)$. 显然 $Y \subset [m, M]$. 而另一方面, $\forall y \in [m,M]$, 由介值定理, $\exists x \in X$ 使得 $f(x) = y$, 这说明 $[m,M]\subset Y$. 故而 $Y = [n,m]$, 也是一个闭区间. Q.E.D.
- 请证明:
a) 如果映射 $f:[0,1]\rightarrow[0,1]$ 连续, $f(0)=0, f(1) = 1$, 并且对于某个 $n\in \mathbb{N}$, 在 $[0,1]$ 上 $f^{n}(x):=(f\circ\cdots\circ f)(x)\equiv x$, 则 $f(x)\equiv x$.
b) 如果不减函数 $f:[0,1]\rightarrow[0,1]$ 连续, 则对于对于任何一个点 $x\in [0,1]$, 以下两种可能的情形中至少可以实现一种: (1) $x$ 是不动点, (2) $f^n(x)$ 趋于不动点.
【证明】
a) 假设 $\exists x \in [0,1]$, 使得 $f(x) = x_1 \neq x$, 而 $x_1$ 不可能是 $f$ 的不动点, 否则 $(f\circ f)(x) = f(x_1) = x_1 = x $ 产生矛盾. 于是令 $(f \circ f)(x) = f(x_1) = x_2$, 同样的 $x_2$ 不可能是 $f$ 的不动点, 并且 $x_2\neq x_1\neq x$ (否则 $x,x_1,x_2$ 都是函数 $f^2(x)$ 的不动点, 若 $n$ 为偶数, 则 $f^{n}(x_1) = x_1 = x$ 产生矛盾; 若 $n$ 为奇数, 则 $f^{n}(x) = f(x) = x_1$ 也矛盾). 一直这样做下去, 到 $f(x_{n-1}) = x_n$ 都不可能是 $f$ 的不动点, 且 $x_n \neq x$, 但这亦与题设矛盾. 故只能有 $f(x)\equiv x$.
b) 由题 4b) 得知函数 $f$ 存在不动点. 设在 $(0,1)$ 共有 $k$ 个不动点, 将定义域分为 $k+1$ 个部分 $[x_i, x_{i+1}], i = 1,\cdots, k, x_0 = 0, x_{k+1}=1$, 在每一段上, 要么 $f(x)>x$, 要么 $f(x)<x$. 不妨设在某一段 $[x_i, x_{i+1}]$ 上 $f(x)<x$, 我们来说明, $f^n(x)$ 趋于 $x_i$. 由于 $f$ 是不减的, 所以 $x_i<f(x)<x<x_{i+1}$, 可知 $\{f^n(x)\}$ 是单调递减有下界的, 故存在极限 $a$, 同时函数连续, $a = \lim_{n\rightarrow \infty}f^n(x) = \lim_{x\rightarrow a}f(x) = f(a)$. 这说明 $a$ 是 $f$ 在 $[x_i, x_{i+1}]$ 上的不动点. 只能有 $a= x_i$.
对于每一段都可以类似证明. 综上, 命题成立. Q.E.D.
- 设 $f:[0,1]\rightarrow \mathbb{R}$ 是连续函数, 并且 $f(0) = f(1)$. 请证明:
a) 对于任何 $n\in \mathbb{N}$, 两端点位于这种函数图像上,且长度等于 $1/n$ 的水平线段存在.
b) 如果数 $l$ 的形式不是 $1/n$, 则可以找到上述形式的函数, 使得在其图像上无法做出长度为 $l$ 的内接水平线.
【证明】
a) 构造函数 $F(x) = f(x-\frac{1}{n})-f(x)$. 显然, $\forall \mathbb{N}\ni x >1$, $F(x)$ 在 $[\frac{1}{n},1]$上连续, 而在其上 $f(x)$ 可以找到 $m$ 和 $M$ 使 $F(x)$ 取得最小值与最大值. 于是
\begin{array}{c}
F(m) = f(m-1/n)-f(m)\geq 0\\
F(M) = f(M-1/n)-f(M)\leq 0.
\end{array}
由介值定理, 必存在 $x_0\in [\frac{1}{n},1]$ 使得 $F(x)=0$. 于是我们证明了命题.
b) 这里, 我们给出一个例子说明. 函数
$$f(x) = \sin^2\left(\frac{\pi x}{l}\right)- x\sin^2\left(\frac{\pi}{l}\right),$$
对于一个形式不是 $1/n$ 的长度 $l$,我们在其图像上无法做出长度为 $l$ 的内接水平线.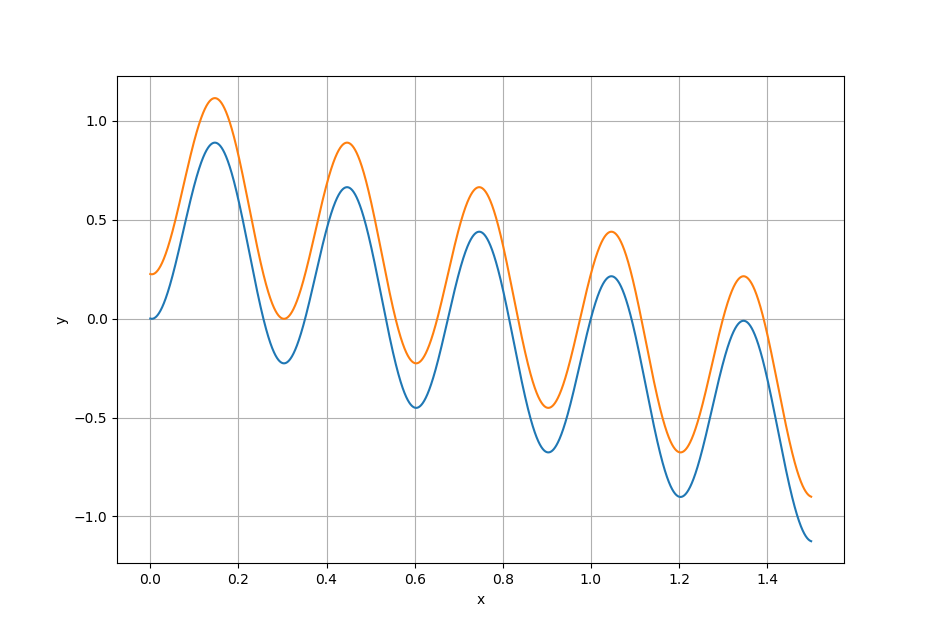
实际上, 做出长度 $l$ 的水平线, 其实相当于将函数图像(向左或向右)平移距离 $l$ 后与原来的函数存在交点. 上图中 $l = 3/10$, 显然其向右平移后的函数与原来的函数并没有焦点. Q.E.D.
数学分析习题解-连续函数(1)

