虎头微分同学的Blog

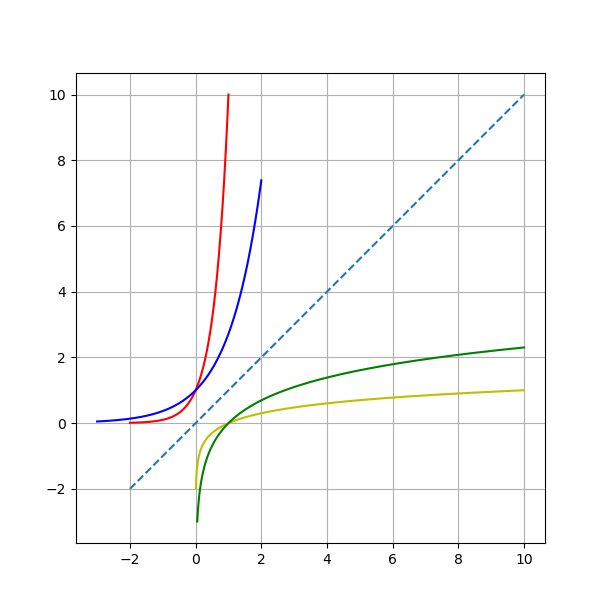
这里, 我们利用实数理论以及极限理论来完整的定义指数函数, 对数函数以及幂函数的定义.

指数函数 $a^x$

设 $a>1$.

1. 对于 $n\in \mathbb{N}$, 归纳的定义 $a^1 = a, a^{n+1}=a^n\cdot a^1$, 这样我们就在 $\mathbb{N}$ 上定义了函数 $a^n$, 同时可以看出, 函数具有性质$a^m/a^n = a^{m-n}(m,n\in \mathbb{N}, m>n)$.
2. 由上面这个性质, 我们可以自然的定义 $a^0: = 1, a^{-n} = 1/a^n$. 于是, $a^n$ 的定义自然的拓展到了整数集 $\mathbb{Z}$ 上. $\forall n,m\in \mathbb{Z}, a^n\cdot a^m = a^{n+m}$.
3. 由实数理论, 我们知道 $\forall a> 0, n\in\mathbb{N},\exists \text{唯一的}x>0 (x^n = a)$. 用 $x = a^{1/n}$ 表示数 $a$ 的 $n$ 次方根. 这一记法保留了指数的加法规则. 于是我们可以进一步定义 $a^{m/n}(m,n\in\mathbb{N})$. 即对于 $r\in\mathbb{Q}$ 定义了 $a^r$.
4. 由归纳原理, 可以验证 $\forall x>0, y>0, n\in\mathbb{N}$ 时有 $(x< y)\Leftrightarrow(x^n< y^n)$ 和 $(x= y)\Leftrightarrow(x^n= y^n)$.
5. 由此我们可以证明有理指数的运算法则, 并得到 $\forall r_1,r_2\in \mathbb{Q}, a^{r_1}\cdot a^{r^2} = a^{r_1+r_2}$.
6. 由 4. 知 $r_1,r_2\in \mathbb{Q}, (r_1<r_2)\Leftrightarrow (a^{r_1}< a^{r^2})$.