关于积拓扑和 Tychonoff 定理
说明. 本文为以前学习拓扑学时的部分笔记, 现发布于博客中供参考备忘. 若有读者发现错漏之处, 敬请电邮联系更正.
首先在集合的层次上讨论积的概念, 然后再转向考虑积拓扑空间, 最后讨论了积空间紧性的问题.
集族的笛卡尔积
Note. 有限个集合的笛卡尔积被定义为有序数组的形式 $(x_1,\cdots,x_n)$, 其中 $x_{i} \in X_{i}$. 也可以将其视为一族 $X_1\times\cdots\times X_2$ 上的映射
$$\left\{x:{1,\cdots,n}\rightarrow X_1\cup\cdots\cup X_n\mid x(j)\in X_{j}, \forall j = 1,\cdots,n \right\}.$$
这个形式方便我们将笛卡尔积推广到一般的集族的情况上.
**定义.**【集族的笛卡尔积】集族 $\{X_{i}\}_{i\in I}$ 的笛卡尔积按如下定义为
$$\prod_{i\in I} X_{i}= \left\{x:I\rightarrow \bigcup_{i\in I}X_{i} \mid x(i)\in X_{i}, \forall i \in I \right\}.$$
对于每个 $x\in \prod_{i\in I} X_{i}$, $x(i)$ 称为 $x$ 的第 $i$ 个坐标, 又可记为 $x_{i}$; 而 $X_{i}$ 称为 $\prod_{i\in I} X_{i}$ 的第 $i$ 个坐标集. 同时, 可以定义从积集到坐标集的映射
$$\begin{eqnarray}
p_{\alpha}: \prod_{i\in I} X_{i} &\longrightarrow& X_\alpha\\
x &\longmapsto& x(\alpha).
\end{eqnarray}$$
称为向第 $\alpha$ 个坐标的投射.
Note. (1) 显然 $X\neq\varnothing \Leftrightarrow X_{i}\neq\varnothing (\forall i\in I)$. 这一点的严格证明用到了选择公理.
(2) 若 $A_{i}\subset X_{i} (i\in I)$, 则有 $\prod_{i\in I} A_{i} \subset \prod_{i\in I} X_{i}$, 可以验证 $\prod_{i\in I} A_{i} = \bigcap p_{i}^{-1}A_{i}$. 取 $A_{i} = X_{i}$, 就容易知道投射 $p_{\alpha}$ 是一个满射.
一般情况的积空间
Note. ${ ( X_{ i },\mathscr{T}_{ i } ) }_{ i \in I }$ 为一族拓扑空间, 考虑其积空间, 要在积集 $X = \prod_{i\in I} X_{i}$ 上定义拓扑, 一个自然的考虑就是希望积空间中的收敛等价于按坐标收敛, 如同在 $\mathbb{R}^n$ 中一样, 而这意味着坐标投射 $p_\alpha$ 应该是一个连续映射, 即对于坐标集中的开集, 在坐标投射下的原象是积集中的开集.
【积拓扑空间】设 ${(X_{i},\mathscr{T}_{i})}_{i\in I}$ 为一族拓扑空间. 定义
\[ \mathscr{B} = \left\{ p_{i}^{-1}(U_{i}) \mid U_{i} \in \mathscr{T}_{i, \forall i\in I \right\}.\]
以 $\mathscr{B}$ 为子基生成的唯一的拓扑 $\mathscr{T}$ 称为 $X = \prod_{i\in I} X_{i}$ 上的积拓扑 $(X,\mathscr{T})$ 称为相应拓扑空间族的积拓扑空间, $X_{i}$ 称为积空间的第 $i$ 个坐标空间.
积拓扑空间由俄罗斯数学家 Tychonoff 在 1930 年代引入.
Note. 【积拓扑的开集结构】
$\mathscr{B}$ 为积拓扑的子基, 其所有的有限子族的交 ${\cap \mathscr{A}\mid \mathscr{A} \subset \mathscr{B} \text{ 有限}}$ 构成了积拓扑的一个基, 记为 $\mathscr{B}^*$. 则 $\forall B\in \mathscr{B}^*$, 具有如下形式
$$B = \bigcap_{k=1}^{n} p_{i_k}^{-1} (U_{i_k})\quad(\text{其中 } U_{i_k}\in \mathscr{T}_{i_k}).$$
其中 ${ i_k }$ 是指标集 $I$ 的一个有限子集. 由集族的笛卡尔积的性质
$\prod_{i\in I} A_{i} = \bigcap p_{i}^{-1}A_{i}$
以及
$X = p_{i}^{-1}X_{i}$,
以上形式又可以改写成
\[B = \prod_{k=1}^{n} B_{i_k}\times \prod_{i\notin {i_k}}X_{i}.\]
若 $I = {1,2,\cdots,n}$ 是一个有限集, 则有
$$B = \prod_{k=1}^{n} B_{k} = \bigcap_{k=1}^{n} p_{k}^{-1} ( U_{k} )\quad(\text{其中 } B_k \in \mathscr{T}_k).$$
这正是有限积空间里的情况.
**定理.**【积拓扑的性质】积拓扑具有以下基本性质:
- $p_\alpha (\alpha\in I)$ 均为连续开映射;
- 对于任意给定的拓扑空间 $Y$, 以及映射
$$f: Y \rightarrow \prod_{ i\in I} X_{i}.$$
则 $f$ 连续当且仅当对于每一个 $\alpha\in I$, $p_{\alpha}\circ f: Y \rightarrow X_\alpha$ 是连续的;- $\mathscr{T}$ 是使得每一个投射 $p_{i}$ 都连续的最小的拓扑;
- 积空间 $X$ 中任意序列 ${ x^{(i)} }_{ i \in \mathbb{Z}_+ }$ 收敛于某 $x\in X$, 当且仅当 $\forall \alpha \in I$, 拓扑空间 $X_{\alpha}$ 中的序列 ${ p_{\alpha}(x^{(i)}) }$ 收敛于 ${ p_{\alpha}(x) }$.
- 若 $A_{i} \subset X_{i} (i\in I)$, 则
$$\overline{ \prod A_{i} } = \prod \overline{ A_{i} },$$
$$\left( \prod A_{i} \right)^{\circ} = \prod A_{i}^{\circ}.$$
上式中若取 $I$ 为有限集, 则直接有结论: 闭集的积集是闭集, 有限个开集的积是开集.
Note. 这些性质的证明类于有限积空间中的证明.
其中 (iii) 说明积拓扑具有某种最小的性质. 而 (ii), (iv) 则说明, 积拓扑空间中的连续和收敛可以被归结为按坐标连续和按坐标收敛, 故积拓扑也被称为坐标式收敛拓扑.
Tychonoff 乘积定理
Note. 紧性是拓扑空间需要研究的重要性质之一. 以下 Tychonoff 乘积定理是拓扑学中的最重要的基本结果之一.
**定理.**【Tychonoff 乘积定理】紧性是可乘的, 即任意一族紧空间的积空间都是紧的.
为了证明这个定理, 首先需要以下定理:
【Alexander 子基定理】
设 $X$ 是一个拓扑空间, $\mathscr{S}$ 是 $X$ 的一个子基, 则 $X$ 是紧的当且仅当由 $\mathscr{S}$ 中的元素构成的 $X$ 的每个覆盖都有一个有限子覆盖.
Note. 利用 Alexander 子基定理, 只要在其子基 $\mathscr{S}$ 的元素构成的任意的 $X$ 的覆盖 $\mathscr{A}$ 中选出有限的子覆盖, 就可以完成证明. 而这是容易的, 总是存在坐标投射 $p_\alpha$, 可以将这个覆盖转化到相应坐标空间 $X_\alpha$ 上的覆盖, 利用坐标空间的紧性, 选出坐标空间上的有限的子族, 对应的也就选出了 $\mathscr{A}$ 中的有限子族覆盖 $X$.
Note. 在多数参考文献中, 为了避免使用使用超限归纳法的繁琐方式, 使用了另一种“对偶”的证明途径, 即, 将寻找有限的子覆盖(元素都是开集)转化为寻找有限个闭集. 而这就启示我们使用有限交性质.
拓扑空间 $X$ 是紧空间 $\Longleftrightarrow$ $X$ 中每一个具有有限交性质的闭集族都有非空的交.
定理的证明也被分成了四步:
- 取一组具有有限交性质的 $X$ 子集族 $\mathscr{A}$, 作为起点;
- 在保持有限交性质的情况下将 $\mathscr{A}$ 扩大; 利用 Zorn 引理, 可以选出一个保持该性质的极大族 $\mathscr{M}$;
- 这个极大族保证了: 通过每个坐标投射 $p_{\alpha}$, $p_\alpha(\mathscr{M})$, 在相应坐标空间 $X_\alpha$ 里面都可以选出元素 $x_{\alpha}\in \bigcap p_\alpha(\mathscr{M})$, 并由此构成的 $X$ 中的元素 $(x_1,\cdots x_{\alpha},\cdots)$ 还落在这个极大族中(一般来说是做不到的, 如下图所示).
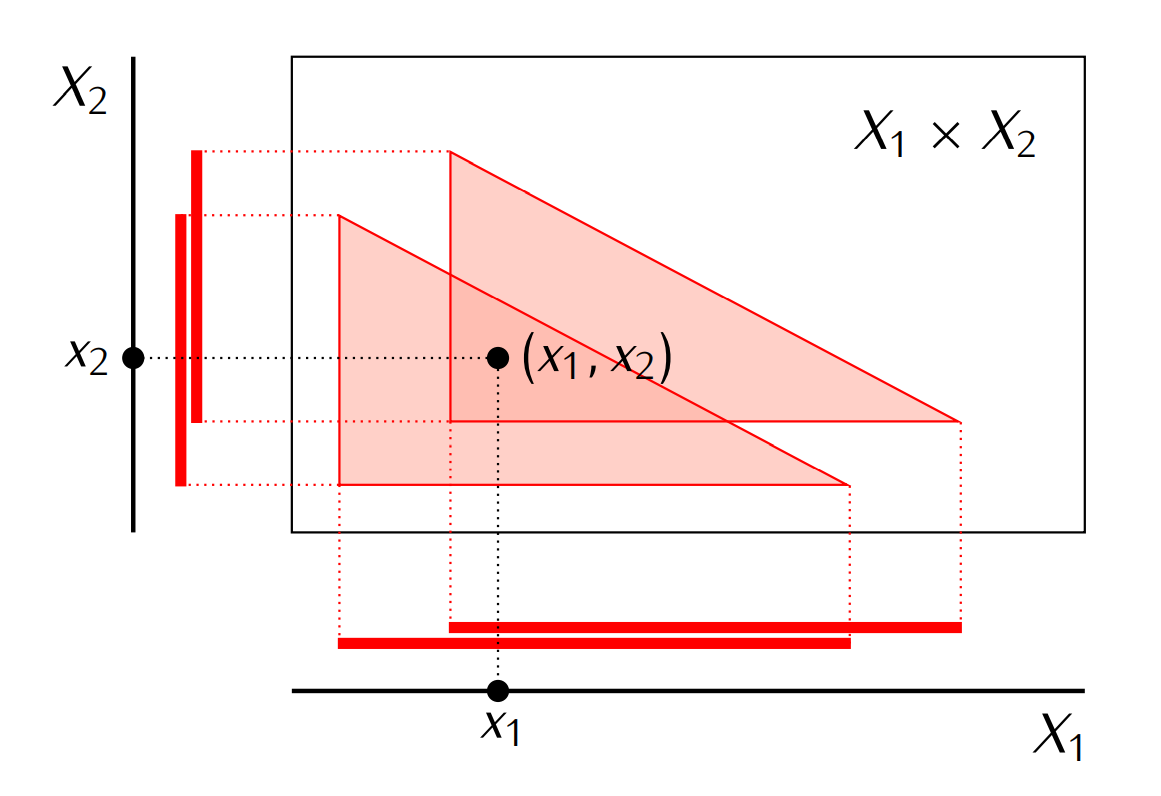
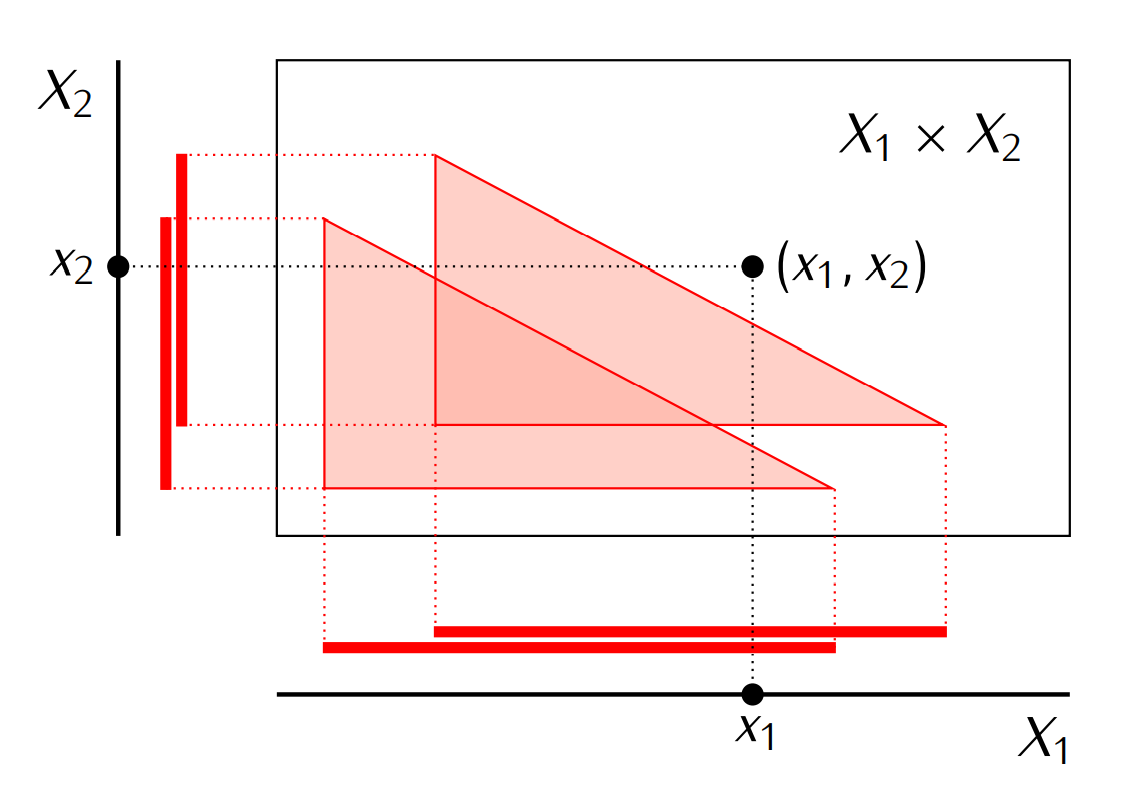
- 因为任意给一组具有有限交性质的子集族 $\mathscr{A}$, 都可以重复以上过程, 这也就可以利用以上的引理完成定理的证明.
关键之处就在于第(2)步, 构造并证明这样“一串”子集族 $\mathscr{A}$ 构成的集合 $\mathbb{A}$, 其中以真包含 $\subsetneq$ 为偏序关系, 满足 Zorn 引理应用的条件.
关于积拓扑和 Tychonoff 定理

